Advertisements
Advertisements
Question
If tan x = `3/4` and `pi < x < (3pi)/2`, then find the value of sin `x/2` and cos `x/2`.
Solution
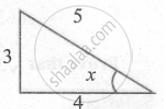
Given tan x = `3/4` and `pi < x < (3pi)/2`
Since x lies in the III quadrant, only tan and its reciprocal are positive.
sin x = `(-3)/5`, cos x = `(-4)/5`.
Now, sin `x/2 = sqrt((1 - cos x)/2) = sqrt(((1 - (-4/5))/2)`
`= sqrt((1 + 4/5)/2)`
`= sqrt(9/10)`
`= 3/sqrt10`
`cos x/2 = sqrt((1 + cos x)/2) = sqrt((1 + 4/5)/2)`
`= sqrt((1 - 4/5)/2) = sqrt(1/10) = 1/sqrt10`
APPEARS IN
RELATED QUESTIONS
Find the value of the following:
cot 75°
Prove that 2 tan 80° = tan 85° – tan 5°.
Prove that:
tan 4A tan 3A tan A + tan 3A + tan A – tan 4A = 0
Prove that `(sin ("B - C"))/(cos "B" cos "C") + (sin ("C - A"))/(cos "C" cos "A") + (sin ("A - B"))/(cos "A" cos "B")` = 0
Prove that cot 4x (sin 5x + sin 3x) = cot x(sin 5x - sin 3x).
Prove that `2 sin^2 (3pi)/4 + 2 cos^2 pi/4 + 2 sec^2 pi/3` = 10
The value of cos(-480°) is:
The value of cos2 45° – sin2 45° is:
The value of 1 – 2 sin2 45° is:
If tan A = `1/2` and tan B = `1/3` then tan(2A + B) is equal to:
