Advertisements
Advertisements
Question
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

Solution
In ΔDOQ and ΔBOP,
∠QDO = ∠PBO ...(Since AB || DC that is, PB || DQ)
So, ∠DOQ = ∠BOP ...(Vertically opposite angles)
`=>` ΔDOQ ∼ ΔBOP ...(AA criterion for similarity)
`=> (DO)/(BO) = (DQ)/(BP)`
`=> (DO)/6 = 8/(BP)`
`=>` BP × DO = 8 × 6 = 48 cm2
APPEARS IN
RELATED QUESTIONS
State, true or false:
The diagonals of a trapezium divide each other into proportional segments.
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
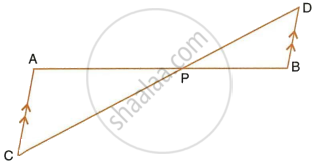
In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
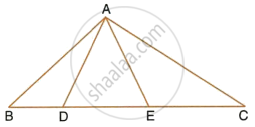
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
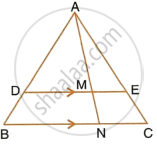
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm.
Calculate:
- EC
- AF
- PE
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In the adjoining figure ABC is a right angle triangle with ∠BAC = 90°, and AD ⊥ BC.
(i) Prove ΔADB ∼ ΔCDA.
(ii) If BD = 18 cm, CD = 8 cm find AD.
(iii) Find the ratio of the area of ΔADB is to area of ΔCDA.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm2, area (ΔDEF) = 25 cm2 and BC = 2·3 cm find EF.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
