Advertisements
Advertisements
Question
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
Solution
We have to prove that ` BP = 1/2 AC`
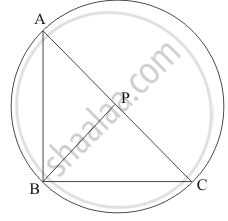
Let Δ ABC be a right angle at B and P be midpoint of AC
Draw a circle with center at P and AC diameter
Since ` angle ABC = ` 90° therefore circle passing through B
So `BP = CP = `radius
`⇒ AP = BP = CP `
Hence
`BP = 1/2 AC` Proved.
APPEARS IN
RELATED QUESTIONS
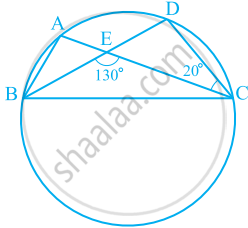
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
Given an arc of a circle, complete the circle.
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
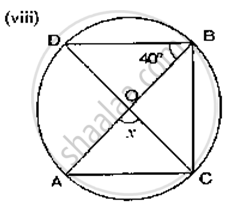
If O is the centre of the circle, find the value of x in the following figure
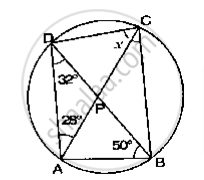
If O is the centre of the circle, find the value of x in the following figures.
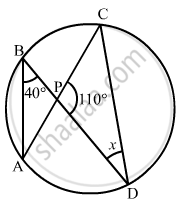
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
In the given figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
