Advertisements
Advertisements
Question
Prove that:
\[\frac{\sin\theta}{\cos(90° - \theta)} + \frac{\cos\theta}{\sin(90° - \theta)} = 2\]
Solution
\[\begin{array}{l}(ii) LHS=\frac{\sin\theta}{\cos( {90}^0 - \theta)} + \frac{\cos\theta}{\sin( {90}^0 - \theta)} \\ \end{array}\]
\[\begin{array}{l}= \frac{\sin\theta}{\sin\theta} + \frac{\cos\theta}{\cos\theta} \\ \end{array}\]
\[\begin{array}{l}= 1 + 1 \\ \end{array}\]
\[\begin{array}{l}= 2 \\ \end{array}\]
\[\begin{array}{l}= \text{RHS} \\ \end{array}\]
\[\begin{array}{l}\text{Hence proved} . \\ \end{array}\]
APPEARS IN
RELATED QUESTIONS
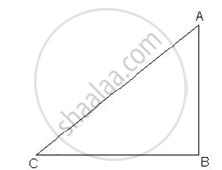
In the below given figure, a tower AB is 20 m high and BC, its shadow on the ground, is 20√3 m long. Find the sun’s altitude.
Without using trigonometric tables, evaluate
`sin^2 34^@ + sin^2 56^@ + 2tan 18^@ tan 72^@ - cot^2 30^@`
Without using tables evaluate: 3cos 80°. cosec 10° + 2sin 59° sec 31°
Without using trigonometric tables, evaluate :
`sin 16^circ/cos 74^circ`
Without using trigonometric tables, evaluate :
`sec 11^circ/("cosec" 79^circ)`
Without using trigonometric tables, evaluate :
`cos 35^circ/sin 55^circ`
Without using trigonometric tables, prove that:
cosec 80° − sec 10° = 0
Without using trigonometric tables, prove that:
cos275° + cos215° = 1
Without using trigonometric tables, prove that:
sin248° + sin242° = 1
Without using trigonometric tables, prove that:
(sin 65° + cos 25°)(sin 65° − cos 25°) = 0
Without using trigonometric tables, prove that:
sin53° cos37° + cos53° sin37° = 1
Prove that:
`cos 80^circ/(sin 10^circ) + cos 59^circ "cosec" 31^circ = 2`
Prove that:
\[\frac{\sin\theta \cos(90^\circ - \theta)\cos\theta}{\sin(90^\circ- \theta)} + \frac{\cos\theta \sin(90^\circ - \theta)\sin\theta}{\cos(90^\circ - \theta)}\]
Prove that:
\[\frac{sin\theta \cos(90° - \theta)cos\theta}{\sin(90° - \theta)} + \frac{cos\theta \sin(90° - \theta)sin\theta}{\cos(90° - \theta)}\]
Without using trigonometric tables, find the value of (sin 72° + cos 18°)(sin 72° - cos 18°).
Using trigonometric table evaluate the following:
cos 64°42' - sin 42°20'
Given that sin θ = `a/b` then cos θ is equal to ______.
Prove that:
`(sin^3 theta + cos^3 theta)/(sin theta + cos theta) = 1 - sin theta cos theta`
