Advertisements
Advertisements
Question
Prove the following: sin230° + cos230° = `(1)/(2)sec60°`
Solution
L.H.S.
= sin230° + cos230°
= `(1/2)^2 + (sqrt(3)/2)^2`
= `(1)/(4) + (3)/(4)`
= `(4)/(4)`
= 1
= `(1)/(2) xx sec60°`
= R.H.S.
APPEARS IN
RELATED QUESTIONS
Use the given figure to find:
(i) tan θ°
(ii) θ°
(iii) sin2θ° - cos2θ°
(iv) Use sin θ° to find the value of x.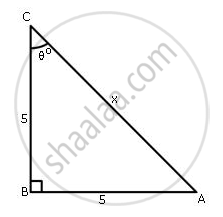
Find the magnitude of angle A, if 2 sin A cos A - cos A - 2 sin A + 1 = 0
Solve the following equation for A, if 2 sin A = 1
Calculate the value of A, if (cosec 2A - 2) (cot 3A - 1) = 0
Solve for x : cos `(x/(2)+10°) = (sqrt3)/(2)`
Solve for x : sin2 60° + cos2 (3x- 9°) = 1
If ΔABC is a right triangle such that ∠C = 90°, ∠A = 45° and BC =7units, find ∠B, AB and AC.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE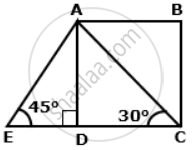
If sin(θ - 15°) = cos(θ - 25°), find the value of θ if (θ-15°) and (θ - 25°) are acute angles.
If secθ= cosec30° and θ is an acute angle, find the value of 4 sin2θ - 2 cos2θ.
