Advertisements
Advertisements
Questions
Show that the time required for 99% completion is double of the time required for the completion of 90% reaction.
For a first-order reaction, derive the relationship t99% = 2t90%.
Solution
For Ist order reaction k = `2.303/"t" log (["A"_0])/(["A"_"t"])`
For 99% completion: If [A0] = 100
[At] = 100 − 99
= 1
∴ t99% = `2.303/"k" log 100/1`
t99% = `2.303/"k" xx 2` .........(1)
∵ log 100 = 2
For 90% completion: If [A0] = 100
[At] = 100 − 90
= 10
t90% = `2.303/"k" log 100/10`
t90% = `2.303/"k"` ...........(2)
∵ log 10 = 1
From (1) and (2),
t99% = 2t90%
APPEARS IN
RELATED QUESTIONS
Calculate the half-life of a first order reaction from the rate constant given below:
200 s−1
The half-life period of zero order reaction A → product is given by
(a) `([A]_0)/k`
(b) `0.693/k`
(c) `[A]_0/(2k)`
(d) `(2[A]_0)/k`
A first order reaction takes 10 minutes for 25% decomposition. Calculate t1/2 for the reaction.
(Given : log 2 = 0.3010, log 3 = 0.4771, log 4 = 0.6021)
Show that for a first order reaction half life is independent of initial concentration.
Which radioactive isotope would have the longer half-life 15O or 19O? (Given rate constants for 15O and 19O are 5.63 × 10–3 s–1 and k = 2.38 × 10–2 s–1 respectively.)
A first-order reaction takes 69.3 min for 50% completion. What is the time needed for 80% of the reaction to get completed? (Given: log 5 = 0.6990, log 8 = 0.9030, log 2 = 0.3010)
Observe the graph shown in figure and answer the following questions:
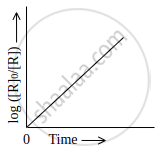
Write the relationship between k and t1/2 (half-life period)
For the given first order reaction A → B the half life of the reaction is 0.3010 min. The ratio of the initial concentration of reactant to the concentration of reactant at time 2.0 min will be equal to ______. (Nearest integer)
Show that the half-life of zero order reaction is `t_(1/2) = ([A]_0)/(2k)`.
Calculate the half-life of a first order reaction from the rate constant given below:
4 year−1
