Advertisements
Advertisements
Question
The minute hand of a clock is 12 cm long. Find the area swept by in it 35 minutes.
Solution
Angle described by the minute hand in 60 minutes = 360°
Angle described by the minute hand in 35 minutes `=(360/60xx35)^circ`
= 210°
Now,
r = 12 cm and θ = 210°
∴ Required area swept by the minute hand in 35 minutes = Area of the sector with r = 12 cm and θ = 210°
`=(pi"r"^2theta)/360`
`=(22/7xx12xx12xx210/360)"cm"^2`
= 264 cm2
APPEARS IN
RELATED QUESTIONS
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
In Figure 5, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR =12 cm. Find the lengths of QM, RN and PL ?

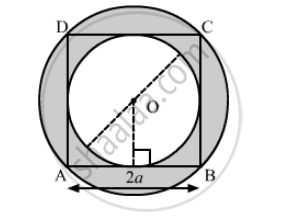
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
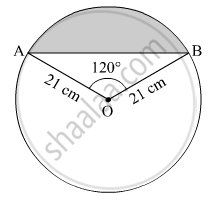
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`