Advertisements
Advertisements
Question
The perimeter of a rhombus is 100 cm and obtuse angle of it is 120°. Find the lengths of its diagonals.
Solution
Consider the following figure,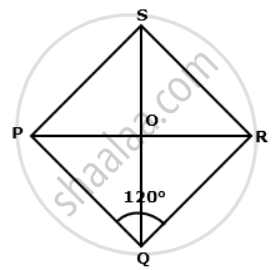
Perimeter of rhombus = 100cm
⇒ PQ = QR = RS = SP = `(100)/(4)` = 25cm
Diagonals of a rhombus bisect each other ar right angles.
⇒ PO = OR and QO = OS
And,
∠POQ = ∠ROQ = ∠ROS = ∠POS = 90°
Also, diagonals bisect the angle at vertex.
⇒ `∠"PQO" = (1)/(2) ∠"POQ" = (1)/(2) xx 120° = 60°`
Now, In right ΔPQR,
sin(∠PQO) = `"OP"/"PQ"`
⇒ sin60° = `"OP"/(25)`
⇒ `sqrt(3)/(2) = "OP"/(25)`
⇒ OP = `(25sqrt(3))/(2)`
∴ PR
= 2 x OP
= `2 xx (25sqrt(3))/(2)`
= `25sqrt(3)"cm"`
Also,
cos(∠PQO) = `"OQ"/"PQ"`
⇒ cos60 = `"OQ"/(25)`
⇒ `(1)/(2) = "OQ"/(25)`
⇒ OQ = `(25)/(2)`
∴ SQ
= 2 x OQ
= `2 xx (25)/(2)`
= 25cm.
APPEARS IN
RELATED QUESTIONS
Solve the following equation for A, if sin 3 A = `sqrt3 /2`
If sin 3A = 1 and 0 < A < 90°, find sin A
In ΔABC, ∠B = 90° , AB = y units, BC = `(sqrt3)` units, AC = 2 units and angle A = x°, find:
- sin x°
- x°
- tan x°
- use cos x° to find the value of y.
Solve the following equations for A, if `sqrt3` tan A = 1
Solve for 'θ': cot2(θ - 5)° = 3
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
If `sqrt(3)` sec 2θ = 2 and θ< 90°, find the value of
cos2 (30° + θ) + sin2 (45° - θ)
Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.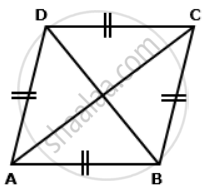
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos84° + cosec69° - cot68°
Evaluate the following: `(sin0° sin35° sin55° sin75°)/(cos22° cos64° cos58° cos90°)`
