Advertisements
Advertisements
प्रश्न
Evaluate the Following
4(sin4 30° + cos2 60°) − 3(cos2 45° − sin2 90°) − sin2 60°
उत्तर
4(sin4 30° + cos2 60°) − 3(cos2 45° − sin2 90°) − sin2 60° .....(i)
By trigonometric ratios we have
`sin 30^@ = 1/2 cos 60^@ = 1/2 cos 45^@ = 1/sqrt2 sin 90^@ = 1 sin 60^@ = sqrt3/2`
By substituting above values in (i), we get
`(4[(1/2)^4 + (1/2)^2]) - 3[[1/sqrt2]^2 - 1] - [sqrt3/2]^2`
`4[1/16 + 1/4] - 3[(1 - [sqrt2])/(sqrt2)^2] - 3/4`
`= 1/4 + 1 - 3/4 + 3/2 = 2`
APPEARS IN
संबंधित प्रश्न
If sec θ = `13/5, "show that" (2sinθ - 3 cosθ)/(4sinθ - 9cosθ) = 3`.
if `tan theta = 12/13` Find `(2 sin theta cos theta)/(cos^2 theta - sin^2 theta)`
if `cos theta = 3/5`, find the value of `(sin theta - 1/(tan theta))/(2 tan theta)`
Evaluate the Following
`(sin 30^@ - sin 90^2 + 2 cos 0^@)/(tan 30^@ tan 60^@)`
Find the value of x in the following :
`2 sin x/2 = 1`
Find the value of x in the following :
`sqrt3 sin x = cos x`
If sin (A − B) = sin A cos B − cos A sin B and cos (A − B) = cos A cos B + sin A sin B, find the values of sin 15° and cos 15°.
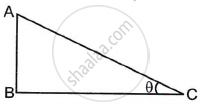
In ΔABC, ∠ABC = 90° and ∠ACB = θ. Then write the ratios of sin θ and tan θ from the figure.
Find the value of sin 45° + cos 45° + tan 45°.
If sec θ = `1/2`, what will be the value of cos θ?
