Advertisements
Advertisements
प्रश्न
Figure shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80 µF, R = 40 Ω.
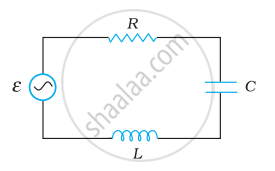
- Determine the source frequency which drives the circuit in resonance.
- Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
- Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
उत्तर
Inductance of the inductor, L = 5.0 H
Capacitance of the capacitor, C = 80 μF = 80 × 10−6 F
Resistance of the resistor, R = 40 Ω
Potential of the variable voltage source, V = 230 V
(a) Resonance angular frequency is given as:
`ω_"R" = 1/sqrt"LC"`
= `1/sqrt (5 xx 80 xx 10^-6)`
= `10^3/20`
= 50 rad s−1
Hence, the circuit will come in resonance for a source frequency of 50 rad s−1.
(b) Impedance of the circuit is given by the relation,
`"Z" = sqrt("R"^2 + (ω"L" - 1/(ω"C"))^2`
At resonance,
`ω"L" = 1/(ω"C")`
∴ Z = R = 40 Ω
Amplitude of the current at the resonating frequency is given as:
`"I"_0 = "V"_0/"Z"`
Where,
V0 = Peak voltage
= `sqrt2 "V"`
∴ `"I"_0 = (sqrt(2) "V")/"Z"`
= `(sqrt2 xx 230)/4`
= 8.13 A
Hence, at resonance, the impedance of the circuit is 40 Ω and the amplitude of the current is 8.13 A.
(c) The rms potential drop across the inductor,
`("V"_"L")_"rms" = "I" xx ω_"R""L"`
Where,
I = rms current
= `"I"_0/sqrt2`
= `(sqrt2 "V")/(sqrt2 "Z")`
= `230/40 "A"`
∴ `("V"_"L")_"rms"= 230/40 xx 50 xx 5`
= 1437.5 V
Potential drop across the capacitor,
`("V"_"c")_"rms" = "I" xx 1/(ω_"R" "C")`
= `230/40 xx 1/(50 xx 80 xx 10^-6)`
= 1437.5 V
Potential drop across the resistor,
`("V"_"R")_"rms" = "IR"`
= `230/40 xx 40`
= 230 V
Potential drop across the LC combination,
`"V"_"LC" = "I" (ω_"R" "L" - 1/(ω_"R" "C"))`
At resonance, ωRL = `1/(ω_"R""C")`
∴ VLC = 0
Hence, it is proved that the potential drop across the LC combination is zero at resonating frequency.
APPEARS IN
संबंधित प्रश्न
A series LCR circuit is connected across an a.c. source of variable angular frequency 'ω'. Plot a graph showing variation of current 'i' as a function of 'ω' for two resistances R1 and R2 (R1 > R2).
Answer the following questions using this graph :
(a) In which case is the resonance sharper and why?
(b) In which case in the power dissipation more and why?
In a series LCR circuit, obtain the condition under which the impedance of the circuit is minimum ?
A series LCR circuit is connected to a source having voltage v = vm sin ωt. Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
Obtain the condition for resonance to occur. Define ‘power factor’. State the conditions under which it is (i) maximum and (ii) minimum.
A coil of resistance 40 Ω is connected across a 4.0 V battery. 0.10 s after the battery is connected, the current in the coil is 63 mA. Find the inductance of the coil.
An inductor-coil of resistance 10 Ω and inductance 120 mH is connected across a battery of emf 6 V and internal resistance 2 Ω. Find the charge which flows through the inductor in (a) 10 ms, (b) 20 ms and (c) 100 ms after the connections are made.
An inductor-coil of inductance 17 mH is constructed from a copper wire of length 100 m and cross-sectional area 1 mm2. Calculate the time constant of the circuit if this inductor is joined across an ideal battery. The resistivity of copper = 1.7 × 10−8 Ω-m.
An LR circuit with emf ε is connected at t = 0. (a) Find the charge Q which flows through the battery during 0 to t. (b) Calculate the work done by the battery during this period. (c) Find the heat developed during this period. (d) Find the magnetic field energy stored in the circuit at time t. (e) Verify that the results in the three parts above are consistent with energy conservation.
Draw a labelled graph showing a variation of impedance of a series LCR circuit with frequency of the a.c. supply.
Use the expression for Lorentz force acting on the charge carriers of a conductor to obtain the expression for the induced emf across the conductor of length l moving with velocity v through a magnetic field B acting perpendicular to its length.
A series LCR circuit with R = 20 Ω, L = 1.5 H and C = 35 µF is connected to a variable-frequency 200 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
Keeping the source frequency equal to the resonating frequency of the series LCR circuit, if the three elements, L, C and R are arranged in parallel, show that the total current in the parallel LCR circuit is minimum at this frequency. Obtain the current rms value in each branch of the circuit for the elements and source specified for this frequency.
For a series LCR-circuit, the power loss at resonance is ______.
A series LCR circuit contains inductance 5 mH, capacitance 2µF and resistance ion. If a frequency A.C. source is varied, what is the frequency at which maximum power is dissipated?
The phase diffn b/w the current and voltage at resonance is
Consider the LCR circuit shown in figure. Find the net current i and the phase of i. Show that i = v/Z`. Find the impedance Z for this circuit.
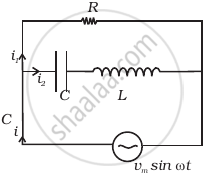
For an LCR circuit driven at frequency ω, the equation reads
`L (di)/(dt) + Ri + q/C = v_i = v_m` sin ωt
- Multiply the equation by i and simplify where possible.
- Interpret each term physically.
- Cast the equation in the form of a conservation of energy statement.
- Integrate the equation over one cycle to find that the phase difference between v and i must be acute.
A series LCR circuit containing a resistance of 120 Ω has angular resonance frequency 4 × 105 rad s-1. At resonance the voltage across resistance and inductance are 60 V and 40 V respectively. At what frequency the current in the circuit lags the voltage by 45°. Give answer in ______ × 105 rad s-1.
When an alternating voltage of 220V is applied across device X, a current of 0.25A flows which lags behind the applied voltage in phase by π/2 radian. If the same voltage is applied across another device Y, the same current flows but now it is in phase with the applied voltage.
- Name the devices X and Y.
- Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.
A series LCR circuit is connected to an ac source. Using the phasor diagram, derive the expression for the impedance of the circuit.
