Advertisements
Advertisements
प्रश्न
Find the equation of the parabola if
the focus is at (0, −3) and the vertex is at (0, 0)
उत्तर
In a parabola, the vertex is the mid-point of the focus and the point of intersection of the axis and the directrix.
Let (x1, y1) be the coordinates of the point of intersection of thIt is given that the vertex and the focus of a parabola are (0, 0) and (0, −3), respectively.
Thus, the slope of the axis of the parabola cannot be defined.
Slope of the directrix = 0
Let the directrix intersect the axis at K (r, s). e axis and directrix.
∴ \[\frac{r + 0}{2} = 0, \frac{s - 3}{2} = 0\]
\[ \Rightarrow r = 0, s = 3\]
∴ Required equation of directrix:
\[y = 3\]
Let P (x, y) be any point on the parabola whose focus is S (0, −3) and the directrix is \[y = 3\]
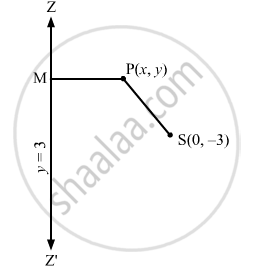 Draw PM perpendicular to \[y = 3\]
Draw PM perpendicular to \[y = 3\]
Then, we have:
\[SP = PM\]
\[ \Rightarrow S P^2 = P M^2 \]
\[ \Rightarrow \left( x - 0 \right)^2 + \left( y + 3 \right)^2 = \left( \frac{y - 3}{\sqrt{1}} \right)^2 \]
\[ \Rightarrow x^2 + y^2 + 6y + 9 = y^2 - 6y + 9\]
\[ \Rightarrow x^2 = - 12y\]
APPEARS IN
संबंधित प्रश्न
Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum.
x2 = 6y
Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum.
y2 = – 8x
Find the equation of the parabola that satisfies the following condition:
Focus (0, –3); directrix y = 3
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0); focus (3, 0)
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0) focus (–2, 0)
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0) passing through (2, 3) and axis is along x-axis
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0), passing through (5, 2) and symmetric with respect to y-axis.
If a parabolic reflector is 20 cm in diameter and 5 cm deep, find the focus.
An equilateral triangle is inscribed in the parabola y2 = 4 ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
Find the equation of the parabola whose:
focus is (0, 0) and the directrix 2x − y − 1 = 0
Find the equation of the parabola if
the focus is at (−6, −6) and the vertex is at (−2, 2)
Find the equation of the parabola if the focus is at (0, −3) and the vertex is at (−1, −3)
Find the equation of the parabola if the focus is at (0, 0) and vertex is at the intersection of the lines x + y = 1 and x − y = 3.
At what point of the parabola x2 = 9y is the abscissa three times that of ordinate?
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest wire being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.
Find the equations of the lines joining the vertex of the parabola y2 = 6x to the point on it which have abscissa 24.
If the points (0, 4) and (0, 2) are respectively the vertex and focus of a parabola, then find the equation of the parabola.
If the line y = mx + 1 is tangent to the parabola y2 = 4x, then find the value of m.
Write the equation of the parabola with focus (0, 0) and directrix x + y − 4 = 0.
The equation of the parabola whose vertex is (a, 0) and the directrix has the equation x + y = 3a, is
The line 2x − y + 4 = 0 cuts the parabola y2 = 8x in P and Q. The mid-point of PQ is
The equation 16x2 + y2 + 8xy − 74x − 78y + 212 = 0 represents
If the coordinates of the vertex and the focus of a parabola are (−1, 1) and (2, 3) respectively, then the equation of its directrix is
The equation of the parabola whose focus is (1, −1) and the directrix is x + y + 7 = 0 is
The equation of the parabola whose focus is the point (2, 3) and directrix is the line x – 4y + 3 = 0 is ______.
Find the coordinates of a point on the parabola y2 = 8x whose focal distance is 4.
Find the length of the line segment joining the vertex of the parabola y2 = 4ax and a point on the parabola where the line segment makes an angle θ to the x-axis.
If the points (0, 4) and (0, 2) are respectively the vertex and focus of a parabola, then find the equation of the parabola.
If the line y = mx + 1 is tangent to the parabola y2 = 4x then find the value of m.
Find the equation of the set of all points the sum of whose distances from the points (3, 0) and (9, 0) is 12.
Find the equation of the set of all points whose distance from (0, 4) are `2/3` of their distance from the line y = 9.
The equation of the parabola having focus at (–1, –2) and the directrix x – 2y + 3 = 0 is ______.
If the vertex of the parabola is the point (–3, 0) and the directrix is the line x + 5 = 0, then its equation is ______.
The equation of the ellipse whose focus is (1, –1), the directrix the line x – y – 3 = 0 and eccentricity `1/2` is ______.
