Advertisements
Advertisements
प्रश्न
Find the co-ordinates of the foot of perpendicular drawn from the point A(1, 8, 4) to the line joining the points B(0, –1, 3) and C(2, –3, –1).
उत्तर
Let L be the foot of perpendicular drawn from the points A (1, 8, 4) to the line passing through B and C as shown in the Figure.
The equation of line BC by using formula `vecr = veca + lambda(vecb - veca)`, the equation of the line BC is
`vecr = (-hatj + 3hatk) + lambda(2hati - 2hatj - 4hatk)`
⇒ `xhati + yhati + xhatk = 2lambdahati - (2lambda + 1)hati + lambda(3 - 4lambda)hatk`
Comparing both sides, we get
`x = 2lambda, y = -(2lambda + 1), z = 3 - 4lambda` ......(1)
Thus, the co-ordinate of L are `(2lambda, -(2lambda + 1), (3 - 4lambda)`
So that the direction ratios of the line AL are `(1 - 2lambda), 8 + (2lambda + 1), 4 - (3 - 4lambda)`
i.e. `1 - 2lambda, 2lambda + 9, 1 + 4lambda`
Since AL is perpendicular to BC, we have
(1 – 2λ) (2 – 0) + (2λ + 9) (–3 + 1) + (4λ + 1) (–1 –3) = 0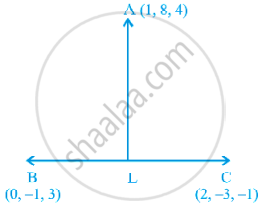
⇒ `lambda = (-5)/6`
The required point is obtained by substituting the value of λ, in (1), which is `((-5)/3, 2/3, 19/3)`.
APPEARS IN
संबंधित प्रश्न
Name the octants in which the following points lie:
(1, 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (–4, 2, –5), (–4, 2, 5),
(–3, –1, 6), (2, –4, –7).
Name the octants in which the following points lie: (5, 2, 3)
Find the image of:
(–5, 4, –3) in the xz-plane.
Find the image of:
(–5, 0, 3) in the xz-plane.
Find the distances of the point P(–4, 3, 5) from the coordinate axes.
Find the point on y-axis which is equidistant from the points (3, 1, 2) and (5, 5, 2).
Show that the points A(3, 3, 3), B(0, 6, 3), C(1, 7, 7) and D(4, 4, 7) are the vertices of a square.
Verify the following:
(–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are vertices of a parallelogram.
Find the locus of the points which are equidistant from the points (1, 2, 3) and (3, 2, –1).
Write the coordinates of the foot of the perpendicular from the point (1, 2, 3) on y-axis.
Find the ratio in which the line segment joining the points (2, 4,5) and (3, −5, 4) is divided by the yz-plane.
The ratio in which the line joining (2, 4, 5) and (3, 5, –9) is divided by the yz-plane is
XOZ-plane divides the join of (2, 3, 1) and (6, 7, 1) in the ratio
The coordinates of the foot of the perpendicular from a point P(6,7, 8) on x - axis are
If the direction ratios of a line are 1, 1, 2, find the direction cosines of the line.
If α, β, γ are the angles that a line makes with the positive direction of x, y, z axis, respectively, then the direction cosines of the line are ______.
If a line makes angles α, β, γ with the positive directions of the coordinate axes, then the value of sin2α + sin2β + sin2γ is ______.
Find the equation of a plane which bisects perpendicularly the line joining the points A(2, 3, 4) and B(4, 5, 8) at right angles.
Two systems of rectangular axis have the same origin. If a plane cuts them at distances a, b, c and a′, b′, c′, respectively, from the origin, prove that
`1/a^2 + 1/b^2 + 1/c^2 = 1/(a"'"^2) + 1/(b"'"^2) + 1/(c"'"^2)`
Show that the points `(hati - hatj + 3hatk)` and `3(hati + hatj + hatk)` are equidistant from the plane `vecr * (5hati + 2hatj - 7hatk) + 9` = 0 and lies on opposite side of it.
Show that the straight lines whose direction cosines are given by 2l + 2m – n = 0 and mn + nl + lm = 0 are at right angles.
If l1, m1, n1 ; l2, m2, n2 ; l3, m3, n3 are the direction cosines of three mutually perpendicular lines, prove that the line whose direction cosines are proportional to l1 + l2 + l3, m1 + m2 + m3, n1 + n2 + n3 makes equal angles with them.
The area of the quadrilateral ABCD, where A(0, 4, 1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2), is equal to ______.
The line `vecr = 2hati - 3hatj - hatk + lambda(hati - hatj + 2hatk)` lies in the plane `vecr.(3hati + hatj - hatk) + 2` = 0.
The vector equation of the line `(x - 5)/3 = (y + 4)/7 = (z - 6)/2` is `vecr = (5hati - 4hatj + 6hatk) + lambda(3hati + 7hatj - 2hatk)`.
If the foot of perpendicular drawn from the origin to a plane is (5, – 3, – 2), then the equation of plane is `vecr.(5hati - 3hatj - 2hatk)` = 38.
