Advertisements
Advertisements
प्रश्न
Find the vector equation of the plane passing through points A (a, 0, 0), B (0, b, 0) and C(0, 0, c). Reduce it to normal form. If plane ABC is at a distance p from the origin, prove that \[\frac{1}{p^2} = \frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2} .\]
उत्तर
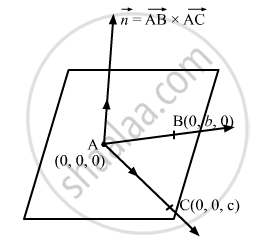
\[ \text{ The required plane passes through the point } A(a, 0, 0) \text{ whose position vector is } \vec{a} =a \hat{i} + 0 \hat{j} + 0 \hat{k} \text{ and is normal to the vector } \vec{n} \text{ given by } \]
\[ \vec{n} = \vec{AB} \times \vec{AC} . \]
\[ \text{ Clearly, } \vec{AB} = \vec{OB} - \vec{OA} = \left( 0 \hat{i} + b \hat{j} + 0 \hat{k} \right) - \left( a \hat{i} + 0 \hat{j} + 0 \hat{k} \right) = - a \hat{i} + b \hat{j} + 0 \hat{k} \]
\[ \vec{AC} = \vec{OC} - \vec{OA} = \left( 0 \hat{i} + 0 \hat{j} + c \hat{k} \right) - \left( a \hat{i} + 0 \hat{j} + 0 \hat{k} \right) = - a \hat{i} + 0 \hat{j} + c \hat{k} \]
\[ \vec{n} = \vec{AB} \times \vec{AC} = \begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ - a & b & 0 \\ - a & 0 & c\end{vmatrix} =\text{bc } \hat{i} + \text{ ac }\hat{j} + \text{ab } \hat{k} \]
\[ \text{ The vector equation of the required plane is } \]
\[ \vec{r} . \vec{n} = \vec{a} . \vec{n} \]
\[ \Rightarrow \vec{r} . \left( \text{ bc }\hat{i} + \text{ac } \hat{j} + \text{ ab } \hat{k} \right) = \left( a \hat{i} + 0 \hat{j} + 0 \hat{ k} \right) . \left( \text{ bc }\hat{i} +\text{ ac }\hat{j} +\text{ ab }\hat{k} \right)\]
\[ \Rightarrow \vec{r} . \left( \text{bc } \hat{i} + \text{ac }\hat{j} + \text{ab }\hat{k} \right) = abc + 0 + 0\]
\[ \Rightarrow \vec{r} . \left( bc \hat{i} + ac \hat{j} + ab \hat{k} \right) = abc . . . \left( 1 \right)\]
\[\text{ Now } ,\left| \vec{n} \right|=\sqrt{\left( bc \right)^2 + \left( ac \right)^2 + \left( ab \right)^2}=\sqrt{b^2 c^2 + a^2 c^2 + a^2 b^2}\]
\[ \text{ For reducing (1) to normal form, we need to divide both sides of (1) by } \sqrt{b^2 c^2 + a^2 c^2 + a^2 b^2}. \text{ Then, we get } \]
\[ \vec{r} . \left( \frac{bc \hat{i} + ac \hat{j} + ab \hat{k} }{\sqrt{b^2 c^2 + a^2 c^2 + a^2 b^2}} \right) = \frac{abc}{\sqrt{b^2 c^2 + a^2 c^2 + a^2 b^2}}, \text{ which is the normal form of plane } (1).\]
\[ \text{ So, the distance of plane (1) from the origin,} \]
\[p = \frac{abc}{\sqrt{b^2 c^2 + a^2 c^2 + a^2 b^2}}, \]
\[ \Rightarrow \frac{1}{p} = \frac{\sqrt{b^2 c^2 + a^2 c^2 + a^2 b^2}}{abc}\]
\[ \Rightarrow \frac{1}{p^2} = \frac{b^2 c^2 + a^2 c^2 + a^2 b^2}{a^2 b^2 c^2}\]
\[ \Rightarrow \frac{1}{p^2} = \frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2}\]
\[\]
APPEARS IN
संबंधित प्रश्न
Find the equation of the plane passing through the point (−1, 3, 2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.
If the points (1, 1, p) and (−3, 0, 1) be equidistant from the plane `vecr.(3hati + 4hatj - 12hatk)+ 13 = 0`, then find the value of p.
Find the vector equation of the line passing through the point (1, 2, − 4) and perpendicular to the two lines:
`(x -8)/3 = (y+19)/(-16) = (z - 10)/7 and (x - 15)/3 = (y - 29)/8 = (z- 5)/(-5)`
Find the vector equation of a plane passing through a point with position vector \[2 \hat{i} - \hat{j} + \hat{k} \] and perpendicular to the vector \[4 \hat{i} + 2 \hat{j} - 3 \hat{k} .\]
Find the Cartesian form of the equation of a plane whose vector equation is
\[\vec{r} \cdot \left( 12 \hat{i} - 3 \hat{j} + 4 \hat{k} \right) + 5 = 0\]
Find the vector equations of the coordinate planes.
\[\vec{n}\] is a vector of magnitude \[\sqrt{3}\] and is equally inclined to an acute angle with the coordinate axes. Find the vector and Cartesian forms of the equation of a plane which passes through (2, 1, −1) and is normal to \[\vec{n}\] .
Show that the normals to the following pairs of planes are perpendicular to each other.
x − y + z − 2 = 0 and 3x + 2y − z + 4 = 0
Find the vector equation of a plane which is at a distance of 3 units from the origin and has \[\hat{k}\] as the unit vector normal to it.
Find the vector equation of the plane passing through the points P (2, 5, −3), Q (−2, −3, 5) and R (5, 3, −3).
Find the vector equation of the plane passing through the points \[3 \hat{i} + 4 \hat{j} + 2 \hat{k} , 2 \hat{i} - 2 \hat{j} - \hat{k} \text{ and } 7 \hat{i} + 6 \hat{k} .\]
Determine the value of λ for which the following planes are perpendicular to each other.
Find the equation of the plane passing through the points whose coordinates are (−1, 1, 1) and (1, −1, 1) and perpendicular to the plane x + 2y + 2z = 5.
Find the equation of the plane that contains the point (1, −1, 2) and is perpendicular to each of the planes 2x + 3y − 2z = 5 and x + 2y − 3z = 8.
Find the equation of the plane passing through (a, b, c) and parallel to the plane \[\vec{r} \cdot \left( \hat{i} + \hat{j} + \hat{k} \right) = 2 .\]
Find the vector equation of the line through the origin which is perpendicular to the plane \[\vec{r} \cdot \left( \hat{i} + 2 \hat{j} + 3 \hat{k} \right) = 3 .\]
Find the vector equation of the line passing through the point (1, −1, 2) and perpendicular to the plane 2x − y + 3z − 5 = 0.
Find the image of the point with position vector \[3 \hat{i} + \hat{j} + 2 \hat{k} \] in the plane \[\vec{r} \cdot \left( 2 \hat{i} - \hat{j} + \hat{k} \right) = 4 .\] Also, find the position vectors of the foot of the perpendicular and the equation of the perpendicular line through \[3 \hat{i} + \hat{j} + 2 \hat{k} .\]
Find the coordinates of the foot of the perpendicular from the point (1, 1, 2) to the plane 2x − 2y + 4z + 5 = 0. Also, find the length of the perpendicular.
Find the image of the point (1, 3, 4) in the plane 2x − y + z + 3 = 0.
Find the coordinates of the foot of the perpendicular and the perpendicular distance of the point P (3, 2, 1) from the plane 2x − y + z + 1 = 0. Also, find the image of the point in the plane.
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x − 3y + 4z − 6 = 0.
Write the ratio in which the plane 4x + 5y − 3z = 8 divides the line segment joining the points (−2, 1, 5) and (3, 3, 2).
Write the intercept cut off by the plane 2x + y − z = 5 on x-axis.
Find the vector equation of the plane, passing through the point (a, b, c) and parallel to the plane \[\vec{r} . \left( \hat{i} + \hat{j} + \hat{k} \right) = 2\]
Find the vector equation of the plane which contains the line of intersection of the planes `vec("r").(hat"i"+2hat"j"+3hat"k"),-4=0, vec("r").(2hat"i"+hat"j"-hat"k")+5=0`and which is perpendicular to the plane`vec("r").(5hat"i"+3hat"j"-6hat"k"),+8=0`
Find the image of the point (1, 6, 3) in the line `x/1 = (y - 1)/2 = (z - 2)/3`.
The coordinates of the foot of the perpendicular drawn from the point (2, 5, 7) on the x-axis are given by ______.
Two systems of rectangular axis have the same origin. If a plane cuts them at distances a, b, c and a′, b′, c′, respectively, from the origin, prove that `1/"a"^2 + 1/"b"^2 + 1/"c"^2 = 1/"a'"^2 + 1/"b'"^2 + 1/"c'"^2`
Find the foot of perpendicular from the point (2, 3, –8) to the line `(4 - x)/2 = y/6 = (1 - z)/3`. Also, find the perpendicular distance from the given point to the line.
The equation of a line, which is parallel to `2hat"i" + hat"j" + 3hat"k"` and which passes through the point (5, –2, 4), is `(x - 5)/2 = (y + 2)/(-1) = (z - 4)/3`.
If the foot of perpendicular drawn from the origin to a plane is (5, – 3, – 2), then the equation of plane is `vec"r".(5hat"i" - 3hat"j" - 2hat"k")` = 38.
The method of splitting a single force into two perpendicular components along x-axis and y-axis is called as ______.
The coordinates of the foot of the perpendicular drawn from the point A(1, 0, 3) to the join of the points B(4, 7, 1) and C(3, 5, 3) are
