Advertisements
Advertisements
प्रश्न
In triangle ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA.
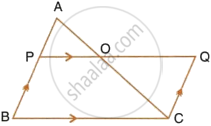
Find:
- area ΔAPO : area ΔABC.
- area ΔAPO : area ΔCQO.
उत्तर
In ΔABC,
AP : PB = 2 : 3
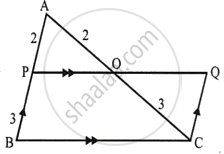
PQ || BC and CQ || BA
∵ PQ || BC
∴ `(AP)/(PB) = (AO)/(OC) = 2/3`
i. In ΔAPQ ∼ ΔABC
∴ `(Area ΔAPO)/(Area ΔABC) = (AP^2)/(AB^2)`
= `(AP^2)/(AP + PB)^2`
= `(2)^2/(2 + 3)^2`
= `4/25`
∴ area ΔAPO : area ΔABC = 4 : 25
ii. In ΔAPO and ΔCQO
∠APO = ∠OQC ...(Alternate angles)
∠AOP = ∠COQ ...(Vertically opposite angles)
∴ ΔAPO ∼ ΔCQO ...(AA axiom)
∴ `(Area ΔAPO)/(Area ΔCQO) = (AP^2)/(CQ^2)`
= `(AP^2)/(PB^2)` {∵ PBCQ is a || gm}
= `(2)^2/(3)^2`
= `4/9`
∴ area ΔAPO : area ΔCQO = 4 : 9
APPEARS IN
संबंधित प्रश्न
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
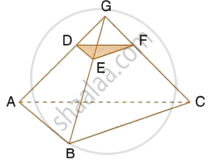
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produces at Q. Given the area of triangle CPQ = 20 cm2.

Calculate:
- area of triangle CDP,
- area of parallelogram ABCD.
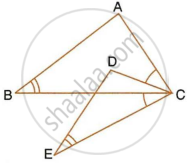
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is
perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:
i)`"area of ADC"/"area of FEB"` ii)`"area of ΔAFEB"/"area of ΔABC"`

In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
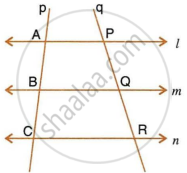
Prove that : `(AB)/(BC) = (PQ)/(QR)`
In the following figure, AB, CD and EF are parallel lines. AB = 6cm, CD = y cm, EF = 10 cm, AC = 4 cm and CF = x cm. Calculate x and y 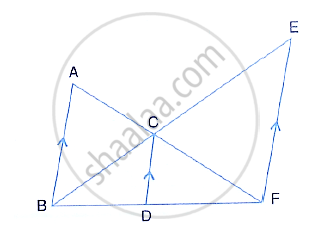
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find:
- the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
- the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
In ΔABC, ∠ACB = 90° and CD ⊥ AB.
Prove that : `(BC^2)/(AC^2)=(BD)/(AD)`
