Advertisements
Advertisements
प्रश्न
O(0, 0), A(6, 0) and B(0, 8) are vertices of a triangle. Find the co-ordinates of the incenter of ∆OAB
उत्तर
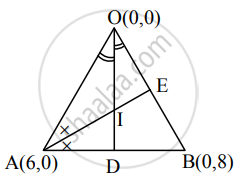
Let bisector of ∠O meet AB at point D and bisector of ∠A meet BO at point E
∴ Point D divides seg AB in the ratio l(OA) : l(OB)
and point E divides seg BO in the ratio l(AB) : l(AO)
Let l be the incentre of ∆OAB.
By distance formula,
l(OA) = `sqrt((0 - 6)^2 + (0 - 0)^2` = 6
l(OB) = `sqrt((0 - 0)^2 + (0 - 8)^2` = 8
∴ Point D divides AB internally in 6 : 8 i.e. 3 : 4
∴ D ≡ `((3(0) + 4(6))/(3 + 4), (3(8) + 4(0))/(3 + 4)) = (24/7, 24/7)`
∴ Equation of OD is `(y - 0)/(24/7 - 0) = (x - 0)/(24/7 - 0)`
∴ y = x ...(i)
Now, by distance formula,
l(AB) = `sqrt((6 - 0)^2 + (0 - 8)^2`
= `sqrt(36 + 64)`
= 10
l(AO) = `sqrt((6 - 0)^2 + (0 - 0)^2` = 6
∴ Point E divides BO internally in 10 : 6 i.e. 5 : 3
∴ E ≡ `((5(0) + 3(0))/(5 + 3), (5(0) + 3(8))/(5 + 3))` ≡ (0, 3)
∴ Equation of AE is `(y - 0)/(3 - 0) = (x - 6)/(0 - 6)`
∴ `y/3 = (x - 6)/(-6)`
∴ –2y = x – 6
∴ x + 2y = 6 ...(ii)
To find co-ordinates of incentre, we have to solve equations (i) and (ii).
Substituting y = x in (ii), we get
x + 2y = 6
∴ x = 2
Substituting the value of x in (i), we get
y = 2
∴ Co-ordinates of incentre I ≡ (2, 2).
Alternate Method: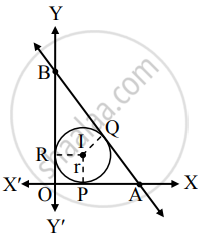
Let I be the incentre.
I lies in the 1st quadrant
OPIR is a square having side length r.
Since OA = 6, OP = r
PA = 6 – r
Since PA = AQ,
AQ = 6 – r …(i)
Since OB = 8, OR = r,
BR = 8 – r
∴ BR = BQ
∴ BQ = 8 – r …(ii)
AB = BQ + AQ
Also, AB = `sqrt("OA"^2 + "OB"^2)`
= `sqrt(6^2 + 8^2)`
= `sqrt(100)`
= 10
∴ BQ + AQ = 10
∴ (8 – r) + (6 – r) = 10 …[From (i) and (ii)]
∴ 2r = 14 – 10 = 4
∴ r = 2
∴ I = (2, 2)
APPEARS IN
संबंधित प्रश्न
Find the slope, X-intercept, Y-intercept of the following line:
3x − y − 9 = 0
Find the slope, X-intercept, Y-intercept of the following line:
x + 2y = 0
Write the following equation in ax + by + c = 0 form.
`x/2 + y/4` = 1
Write the following equation in ax + by + c = 0 form.
`x/3 - y/2` = 0
Show that lines x – 2y – 7 = 0 and 2x − 4y + 15 = 0 are parallel to each other
Show that lines x − 2y − 7 = 0 and 2x + y + 1 = 0 are perpendicular to each other. Find their point of intersection
If the line 3x + 4y = p makes a triangle of area 24 square unit with the co-ordinate axes then find the value of p.
Find the co-ordinates of the foot of the perpendicular drawn from the point A(–2, 3) to the line 3x – y – 1 = 0
Find the co-ordinates of the circumcenter of the triangle whose vertices are A(–2, 3), B(6, –1), C(4, 3).
Find the co-ordinates of the orthocenter of the triangle whose vertices are A(3, –2), B(7, 6), C(–1, 2).
Show that lines 3x − 4y + 5 = 0, 7x − 8y + 5 = 0, and 4x + 5y − 45 = 0 are concurrent. Find their point of concurrence
Find the equation of the line whose X-intercept is 3 and which is perpendicular to the line 3x − y + 23 = 0.
Find the distance of the origin from the line 7x + 24y – 50 = 0
Find points on the line x + y − 4 = 0 which are at one unit distance from the line 4x + 3y – 10 = 0.
Find the equation of the line parallel to the X-axis and passing through the point of intersection of lines x + y − 2 = 0 and 4x + 3y = 10
D(−1, 8), E(4, −2), F(−5, −3) are midpoints of sides BC, CA and AB of ∆ABC Find equations of sides of ∆ABC
Answer the following question:
Find the distance of the origin from the line x = – 2
Answer the following question:
Obtain the equation of the line which is parallel to the X−axis and making an intercept of 5 on the Y−axis.
Answer the following question:
Obtain the equation of the line which is parallel to the Y−axis and making an intercept of 3 on the X−axis.
Answer the following question:
Find the distance between the parallel lines 3x + 4y + 3 = 0 and 3x + 4y + 15 = 0
Answer the following question:
Find the equation of the line which passes through the point of intersection of lines x + y + 9 = 0, 2x + 3y + 1 = 0 and which makes X-intercept 1.
Answer the following question:
Find the distance of the line 4x − y = 0 from the point P(4, 1) measured along the line making an angle of 135° with the positive X-axis
The length of perpendicular from (1, 3) on line 3x + 4y + 10 = 0, is ______
The y-intercept of the line passing through A( 6, 1) and perpendicular to the line x - 2y = 4 is ______.
Let the straight line x = b divide the area enclosed by y = (1 - x)2, y = 0 and x = 0 into two parts R1(0 ≤ x ≤ b) and R2 (b ≤ x ≤ 1) such that `R_1 - R_2 = 1/4`. Then b equals ______
The equation 3x2 - 4xy + y2 = 0 represent a pair of straight lines whose slopes differ by ______.
If a plane has x-intercept l, y-intercept m and z-intercept n, and perpendicular distance of plane from the origin is k, then _______.
The length of the perpendicular from the origin on the line `(xsinalpha)/"b" - (ycosalpha)/"a" - 1 = 0` is ______.
