Advertisements
Advertisements
प्रश्न
Show that the function f : Q → Q, defined by f(x) = 3x + 5, is invertible. Also, find f−1
उत्तर
Injectivity of f:
Let x and y be two elements of the domain (Q), such that
f(x)=f(y)
⇒ 3x + 5 =3y + 5
⇒ 3x = 3y
⇒ x = y
So, f is one-one.
Surjectivity of f:
Let y be in the co-domain (Q), such that f(x) = y
⇒ 3x +5 = y
⇒ 3x = y - 5
⇒ `x = (y -5)/3 in` (domain)
⇒ f is onto.
So, f is a bijection and, hence, it is invertible.
Finding f-1:
Let f−1(x)=y ...(1)
⇒ x=f(y)
⇒ x=3y+5
⇒ x −5 = 3y
⇒ `y = (x -5)/3`
So, `f^-1 (x) = (x-5)/3` [from (1)]
APPEARS IN
संबंधित प्रश्न
Let f: N → N be defined by f(n) = `{((n+1)/2, ",if n is odd"),(n/2,",n is even"):}` for all n ∈ N.
State whether the function f is bijective. Justify your answer.
Let f: R → R be defined as f(x) = x4. Choose the correct answer.
Given examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.
(Hint: Consider f(x) = x + 1 and `g(x) = {(x-1, ifx >1),(1, if x = 1):}`
Prove that the function f : N → N, defined by f(x) = x2 + x + 1, is one-one but not onto
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = x3 − x
Let A = [-1, 1]. Then, discuss whether the following functions from A to itself is one-one, onto or bijective : h(x) = x2
If f : R → R be the function defined by f(x) = 4x3 + 7, show that f is a bijection.
If A = {1, 2, 3}, show that a one-one function f : A → A must be onto.
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + x2 and g(x) = x3
If f : A → B and g : B → C are one-one functions, show that gof is a one-one function.
if `f (x) = sqrt(1-x)` and g(x) = `log_e` x are two real functions, then describe functions fog and gof.
If f : R → (−1, 1) defined by `f (x) = (10^x- 10^-x)/(10^x + 10 ^-x)` is invertible, find f−1.
If f : C → C is defined by f(x) = x4, write f−1 (1).
If f : R → R defined by f(x) = 3x − 4 is invertible, then write f−1 (x).
Let f : R → R, g : R → R be two functions defined by f(x) = x2 + x + 1 and g(x) = 1 − x2. Write fog (−2).
Write whether f : R → R, given by `f(x) = x + sqrtx^2` is one-one, many-one, onto or into.
Let f, g : R → R be defined by f(x) = 2x + l and g(x) = x2−2 for all x
∈ R, respectively. Then, find gof. [NCERT EXEMPLAR]
The function \[f : [0, \infty ) \to \text {R given by } f\left( x \right) = \frac{x}{x + 1} is\]
The range of the function
\[f\left( x \right) =^{7 - x} P_{x - 3}\]
Which of the following functions from
to itself are bijections?
The function
\[f : R \to R\] defined by\[f\left( x \right) = \left( x - 1 \right) \left( x - 2 \right) \left( x - 3 \right)\]
(a) one-one but not onto
(b) onto but not one-one
(c) both one and onto
(d) neither one-one nor onto
The function \[f : R \to R\] defined by
\[f\left( x \right) = 6^x + 6^{|x|}\] is
Let
\[A = \left\{ x \in R : x \geq 1 \right\}\] The inverse of the function,
\[f : A \to A\] given by
\[f\left( x \right) = 2^{x \left( x - 1 \right)} , is\]
Consider the set A containing n elements. Then, the total number of injective functions from A onto itself is ______
Let f: R → R be the function defined by f(x) = 2x – 3 ∀ x ∈ R. write f–1
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
k = {(1,4), (2, 5)}
Using the definition, prove that the function f: A→ B is invertible if and only if f is both one-one and onto
Let f: R → R be given by f(x) = tan x. Then f–1(1) is ______.
Let A = {0, 1} and N be the set of natural numbers. Then the mapping f: N → A defined by f(2n – 1) = 0, f(2n) = 1, ∀ n ∈ N, is onto.
The number of bijective functions from set A to itself when A contains 106 elements is ____________.
The domain of the function `"f"("x") = 1/(sqrt ({"sin x"} + {"sin" ( pi + "x")}))` where {.} denotes fractional part, is
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let f: R → R be defined by f(x) = x2 is:
Let n(A) = 4 and n(B) = 6, Then the number of one – one functions from 'A' to 'B' is:
Function f: R → R, defined by f(x) = `x/(x^2 + 1)` ∀ x ∈ R is not
If A = {x ∈ R: |x – 2| > 1}, B = `{x ∈ R : sqrt(x^2 - 3) > 1}`, C = {x ∈ R : |x – 4| ≥ 2} and Z is the set of all integers, then the number of subsets of the set (A ∩ B ∩ C) C ∩ Z is ______.
Let A = {1, 2, 3, ..., 10} and f : A `rightarrow` A be defined as
f(k) = `{{:(k + 1, if k "is odd"),( k, if k "is even"):}`.
Then the number of possible functions g : A `rightarrow` A such that gof = f is ______.
A function f : [– 4, 4] `rightarrow` [0, 4] is given by f(x) = `sqrt(16 - x^2)`. Show that f is an onto function but not a one-one function. Further, find all possible values of 'a' for which f(a) = `sqrt(7)`.
Which one of the following graphs is a function of x?
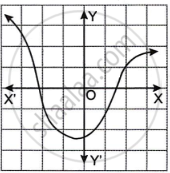 |
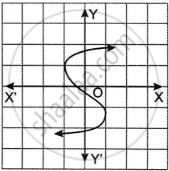 |
| Graph A | Graph B |
If f : R `rightarrow` R is defined by `f(x) = (2x - 7)/4`, show that f(x) is one-one and onto.
