Advertisements
Advertisements
प्रश्न
Let f : R → R, g : R → R be two functions defined by f(x) = x2 + x + 1 and g(x) = 1 − x2. Write fog (−2).
उत्तर
\[\left( fog \right)\left( - 2 \right) = f \left( g \left( - 2 \right) \right)\]
\[ = f\left( 1 - \left( - 2 \right)^2 \right)\]
\[ = f\left( - 3 \right)\]
\[ = \left( - 3 \right)^2 + \left( - 3 \right) + 1\]
\[ = 9 - 3 + 1\]
\[ = 7\]
APPEARS IN
संबंधित प्रश्न
Show that the function f in `A=R-{2/3} ` defined as `f(x)=(4x+3)/(6x-4)` is one-one and onto hence find f-1
Show that the modulus function f: R → R given by f(x) = |x| is neither one-one nor onto, where |x| is x, if x is positive or 0 and |x| is − x if x is negative.
Show that function f: R `rightarrow` {x ∈ R : −1 < x < 1} defined by f(x) = `x/(1 + |x|)`, x ∈ R is one-one and onto function.
Let S = {a, b, c} and T = {1, 2, 3}. Find F−1 of the following functions F from S to T, if it exists.
F = {(a, 3), (b, 2), (c, 1)}
Prove that the function f : N → N, defined by f(x) = x2 + x + 1, is one-one but not onto
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = `x/(x^2 +1)`
Set of ordered pair of a function ? If so, examine whether the mapping is injective or surjective :{(a, b) : a is a person, b is an ancestor of a}
Let f : R → R and g : R → R be defined by f(x) = x2 and g(x) = x + 1. Show that fog ≠ gof.
Consider f : N → N, g : N → N and h : N → R defined as f(x) = 2x, g(y) = 3y + 4 and h(z) = sin z for all x, y, z ∈ N. Show that ho (gof) = (hog) of.
If f : A → B and g : B → C are onto functions, show that gof is a onto function.
Find fog and gof if : f(x) = sin−1 x, g(x) = x2
Find fog and gof if : f (x) = x+1, g (x) = sin x .
Find fog and gof if : f(x) = c, c ∈ R, g(x) = sin `x^2`
Let f : R `{- 4/3} `- 43 →">→ R be a function defined as f(x) = `(4x)/(3x +4)` . Show that f : R - `{-4/3}`→ Rang (f) is one-one and onto. Hence, find f -1.
If f : R → R is defined by f(x) = x2, find f−1 (−25).
Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\] be a function defined by f(x) = cos [x]. Write range (f).
What is the range of the function
`f (x) = ([x - 1])/(x -1) ?`
A function f from the set of natural numbers to the set of integers defined by
\[f\left( n \right)\begin{cases}\frac{n - 1}{2}, & \text{when n is odd} \\ - \frac{n}{2}, & \text{when n is even}\end{cases}\]
If \[f : R \to R is given by f\left( x \right) = 3x - 5, then f^{- 1} \left( x \right)\]
Let
\[f : [2, \infty ) \to X\] be defined by
\[f\left( x \right) = 4x - x^2\] Then, f is invertible if X =
If \[f\left( x \right) = \sin^2 x\] and the composite function \[g\left( f\left( x \right) \right) = \left| \sin x \right|\] then g(x) is equal to
Mark the correct alternative in the following question:
Let f : R→ R be defined as, f(x) = \[\begin{cases}2x, if x > 3 \\ x^2 , if 1 < x \leq 3 \\ 3x, if x \leq 1\end{cases}\]
Then, find f( \[-\]1) + f(2) + f(4)
Mark the correct alternative in the following question:
If the set A contains 5 elements and the set B contains 6 elements, then the number of one-one and onto mappings from A to B is
If f(x) = `(x+3)/(4x−5) , "g"(x) = (3+5x)/(4x−1)` then verify that `("fog") (x)` = x.
Write about strcmp() function.
Set A has 3 elements and the set B has 4 elements. Then the number of injective mappings that can be defined from A to B is ______.
Let f: R → R be defined by f(x) = 3x – 4. Then f–1(x) is given by ______.
For sets A, B and C, let f: A → B, g: B → C be functions such that g o f is injective. Then both f and g are injective functions.
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
g = {(1, 4), (2, 4), (3, 4)}
Let f: R → R be the functions defined by f(x) = x3 + 5. Then f–1(x) is ______.
If f(x) = (4 – (x – 7)3}, then f–1(x) = ______.
Let f : R `->` R be a function defined by f(x) = x3 + 4, then f is ______.
Let f : R → R, g : R → R be two functions such that f(x) = 2x – 3, g(x) = x3 + 5. The function (fog)-1 (x) is equal to ____________.
The function f: R → R defined as f(x) = x3 is:
A general election of Lok Sabha is a gigantic exercise. About 911 million people were eligible to vote and voter turnout was about 67%, the highest ever

Let I be the set of all citizens of India who were eligible to exercise their voting right in the general election held in 2019. A relation ‘R’ is defined on I as follows:
R = {(V1, V2) ∶ V1, V2 ∈ I and both use their voting right in the general election - 2019}
- Three friends F1, F2, and F3 exercised their voting right in general election-2019, then which of the following is true?
Let the function f: R → R be defined by f(x) = 4x – 1, ∀ x ∈ R then 'f' is
Difference between the greatest and least value of f(x) = `(1 + (cos^-1x)/π)^2 - (1 + (sin^-1x)/π)^2` is ______.
Let x is a real number such that are functions involved are well defined then the value of `lim_(t→0)[max{(sin^-1 x/3 + cos^-1 x/3)^2, min(x^2 + 4x + 7)}]((sin^-1t)/t)` where [.] is greatest integer function and all other brackets are usual brackets.
ASSERTION (A): The relation f : {1, 2, 3, 4} `rightarrow` {x, y, z, p} defined by f = {(1, x), (2, y), (3, z)} is a bijective function.
REASON (R): The function f : {1, 2, 3} `rightarrow` {x, y, z, p} such that f = {(1, x), (2, y), (3, z)} is one-one.
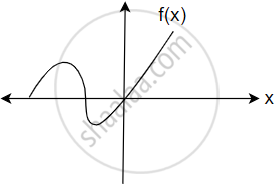
The given function f : R → R is not ‘onto’ function. Give reason.
