Advertisements
Advertisements
प्रश्न
The area of the quadrilateral ABCD, where A(0,4,1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2), is equal to ______.
विकल्प
9 sq.units
18 sq.units
27 sq.units
81 sq.units
उत्तर
The area of the quadrilateral ABCD, where A(0,4,1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2), is equal to 9 sq.units.
Explanation:
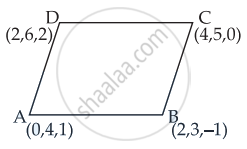
Given points are A(0, 4, 1), B(2,3,– 1), C(4, 5, 0) and D(2,6,2)
D’ratios of AB = 2,–1 –2
And d’ratios of DC = 2,–1,–2
∴ AB||DC
Similarly, d’ratios of AD = 2, 2, 1 and d’ratios of BC = 2, 2, 1
∴ AD || BC
So ABCD is a parallelogram
`vec"AB" = 2hat"i" - hat"j" - 2hat"k"`
`vec"AD" = 2hat"i" + 2hat"j" + hat"k"`
∴ Area of parallelogram ABCD = `|vec"AB" xx vec"AD"|`
= `|(hat"i", hat"j", hat"k"),(2, -1, -2),(2, 2, 1)|`
= `hat"i"(-1 + 4) - hat"j"(2 + 4) + hat"k"(4 + 2)`
= `3hat"i" - 6hat"j" + 6hat"k"`
= `sqrt((3)^2 + (-6)^2 + (6)^2)`
= `sqrt(9 + 36 + 36)`
= `sqrt(81)`
= 9 sq.units
APPEARS IN
संबंधित प्रश्न
Find the direction cosines of the line perpendicular to the lines whose direction ratios are -2, 1,-1 and -3, - 4, 1
If a line makes angles of 90°, 60° and 30° with the positive direction of x, y, and z-axis respectively, find its direction cosines
Find the direction cosines of the line passing through two points (−2, 4, −5) and (1, 2, 3) .
Find the angle between the vectors with direction ratios proportional to 1, −2, 1 and 4, 3, 2.
Show that the points (2, 3, 4), (−1, −2, 1), (5, 8, 7) are collinear.
Show that the line through points (4, 7, 8) and (2, 3, 4) is parallel to the line through the points (−1, −2, 1) and (1, 2, 5).
If the coordinates of the points A, B, C, D are (1, 2, 3), (4, 5, 7), (−4, 3, −6) and (2, 9, 2), then find the angle between AB and CD.
Find the angle between the lines whose direction cosines are given by the equations
l + 2m + 3n = 0 and 3lm − 4ln + mn = 0
What are the direction cosines of Y-axis?
What are the direction cosines of Z-axis?
If a line makes angles α, β and γ with the coordinate axes, find the value of cos2α + cos2β + cos2γ.
Write the inclination of a line with Z-axis, if its direction ratios are proportional to 0, 1, −1.
Write the distance of the point P (x, y, z) from XOY plane.
Find the distance of the point (2, 3, 4) from the x-axis.
For every point P (x, y, z) on the x-axis (except the origin),
The distance of the point P (a, b, c) from the x-axis is
Ratio in which the xy-plane divides the join of (1, 2, 3) and (4, 2, 1) is
The angle between the two diagonals of a cube is
Verify whether the following ratios are direction cosines of some vector or not
`1/5, 3/5, 4/5`
Verify whether the following ratios are direction cosines of some vector or not
`4/3, 0, 3/4`
If (a, a + b, a + b + c) is one set of direction ratios of the line joining (1, 0, 0) and (0, 1, 0), then find a set of values of a, b, c
If a line makes an angle of 30°, 60°, 90° with the positive direction of x, y, z-axes, respectively, then find its direction cosines.
If a line makes angles `pi/2, 3/4 pi` and `pi/4` with x, y, z axis, respectively, then its direction cosines are ______.
If a line makes angles α, β, γ with the positive directions of the coordinate axes, then the value of sin2α + sin2β + sin2γ is ______.
O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.
If a line makes angles 90°, 135°, 45° with x, y and z-axis respectively then which of the following will be its direction cosine.
A line passes through the points (6, –7, –1) and (2, –3, 1). The direction cosines of the line so directed that the angle made by it with positive direction of x-axis is acute, are ______.
If the equation of a line is x = ay + b, z = cy + d, then find the direction ratios of the line and a point on the line.
