Advertisements
Advertisements
प्रश्न
The area of the quadrilateral ABCD, where A(0,4,1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2), is equal to ______.
पर्याय
9 sq.units
18 sq.units
27 sq.units
81 sq.units
उत्तर
The area of the quadrilateral ABCD, where A(0,4,1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2), is equal to 9 sq.units.
Explanation:
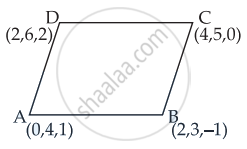
Given points are A(0, 4, 1), B(2,3,– 1), C(4, 5, 0) and D(2,6,2)
D’ratios of AB = 2,–1 –2
And d’ratios of DC = 2,–1,–2
∴ AB||DC
Similarly, d’ratios of AD = 2, 2, 1 and d’ratios of BC = 2, 2, 1
∴ AD || BC
So ABCD is a parallelogram
`vec"AB" = 2hat"i" - hat"j" - 2hat"k"`
`vec"AD" = 2hat"i" + 2hat"j" + hat"k"`
∴ Area of parallelogram ABCD = `|vec"AB" xx vec"AD"|`
= `|(hat"i", hat"j", hat"k"),(2, -1, -2),(2, 2, 1)|`
= `hat"i"(-1 + 4) - hat"j"(2 + 4) + hat"k"(4 + 2)`
= `3hat"i" - 6hat"j" + 6hat"k"`
= `sqrt((3)^2 + (-6)^2 + (6)^2)`
= `sqrt(9 + 36 + 36)`
= `sqrt(81)`
= 9 sq.units
APPEARS IN
संबंधित प्रश्न
Find the direction cosines of a line which makes equal angles with the coordinate axes.
Find the Direction Cosines of the Sides of the triangle Whose Vertices Are (3, 5, -4), (-1, 1, 2) and (-5, -5, -2).
If the lines `(x-1)/(-3) = (y -2)/(2k) = (z-3)/2 and (x-1)/(3k) = (y-1)/1 = (z -6)/(-5)` are perpendicular, find the value of k.
Find the angle between the vectors whose direction cosines are proportional to 2, 3, −6 and 3, −4, 5.
Show that the points (2, 3, 4), (−1, −2, 1), (5, 8, 7) are collinear.
Show that the line through points (4, 7, 8) and (2, 3, 4) is parallel to the line through the points (−1, −2, 1) and (1, 2, 5).
Show that the line through the points (1, −1, 2) and (3, 4, −2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Find the direction cosines of the lines, connected by the relations: l + m +n = 0 and 2lm + 2ln − mn= 0.
Find the angle between the lines whose direction cosines are given by the equations
l + 2m + 3n = 0 and 3lm − 4ln + mn = 0
Define direction cosines of a directed line.
Write the ratio in which YZ-plane divides the segment joining P (−2, 5, 9) and Q (3, −2, 4).
A line makes an angle of 60° with each of X-axis and Y-axis. Find the acute angle made by the line with Z-axis.
Write the inclination of a line with Z-axis, if its direction ratios are proportional to 0, 1, −1.
Find the distance of the point (2, 3, 4) from the x-axis.
Write direction cosines of a line parallel to z-axis.
A rectangular parallelopiped is formed by planes drawn through the points (5, 7, 9) and (2, 3, 7) parallel to the coordinate planes. The length of an edge of this rectangular parallelopiped is
If the x-coordinate of a point P on the join of Q (2, 2, 1) and R (5, 1, −2) is 4, then its z-coordinate is
Find the equation of the lines passing through the point (2, 1, 3) and perpendicular to the lines
If a line makes angles 90°, 135°, 45° with the x, y and z axes respectively, find its direction cosines.
Find the vector equation of a line passing through the point (2, 3, 2) and parallel to the line `vec("r") = (-2hat"i"+3hat"j") +lambda(2hat"i"-3hat"j"+6hat"k").`Also, find the distance between these two lines.
Find the direction cosines and direction ratios for the following vector
`3hat"i" - 4hat"j" + 8hat"k"`
Find the direction cosines and direction ratios for the following vector
`3hat"i" + hat"j" + hat"k"`
A triangle is formed by joining the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). Find the direction cosines of the medians
If a variable line in two adjacent positions has direction cosines l, m, n and l + δl, m + δm, n + δn, show that the small angle δθ between the two positions is given by δθ2 = δl2 + δm2 + δn2
O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.
If a line makes angles 90°, 135°, 45° with x, y and z-axis respectively then which of the following will be its direction cosine.
What will be the value of 'P' so that the lines `(1 - x)/3 = (7y - 14)/(2P) = (z - 3)/2` and `(7 - 7x)/(3P) = (y - 5)/1 = (6 - z)/5` at right angles.
A line in the 3-dimensional space makes an angle θ `(0 < θ ≤ π/2)` with both the x and y axes. Then the set of all values of θ is the interval ______.
The projections of a vector on the three coordinate axis are 6, –3, 2 respectively. The direction cosines of the vector are ______.
