Advertisements
Advertisements
प्रश्न
The maximum value of `[x(x −1) +1]^(1/3)` , 0 ≤ x ≤ 1 is ______.
विकल्प
`(1/3)^(1/3)`
`1/2`
1
0
उत्तर
The maximum value of `[x(x −1) +1]^(1/3)` , 0 ≤ x ≤ 1 is 1.
Explanation:
Let, `y = [x (x – 1) + 1]^(1/3)`
Differentiating both sides with respect to x,
`dy/dx = 1/3 [x (x - 1) + 1]^(-2/3) d/dx [x(x - 1) + 1]`
`= 1/3 [x (x - 1) + 1]^(-2/3) × (2x - 1)`
`= (2x - 1)/(3 [x (x - 1) + 1]^(2/3))`
For highest and lowest value, `dy/dx = 0 => 2x - 1 = 0 => x = 1/2`
For highest and lowest value, `dy/dx = 0 => 2x - 1 = 0 => x = 1/2`
At `x= 0, f(0) = 1^(1/3) = 1`
At `x= 1, f(1) = 1^(1/3) = 1`
x `= 1/2 at, f(1/2) = [1/2 (-1/2) xx 1]^(1/3) = (3/4)^(1/3)`
`dy/dx , at x = 1/2` sign is changing from -ve to +ve
∴ y is minimum at x = `1/2`.
maximum value = 1
APPEARS IN
संबंधित प्रश्न
If `f'(x)=k(cosx-sinx), f'(0)=3 " and " f(pi/2)=15`, find f(x).
An open box is to be made out of a piece of a square card board of sides 18 cms by cutting off equal squares from the comers and turning up the sides. Find the maximum volume of the box.
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π/3.
Find the maximum and minimum value, if any, of the following function given by f(x) = (2x − 1)2 + 3.
Find the maximum and minimum value, if any, of the following function given by f(x) = 9x2 + 12x + 2
Find the maximum and minimum value, if any, of the following function given by g(x) = − |x + 1| + 3.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
g(x) = x3 − 3x
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`h(x) = sinx + cosx, 0 < x < pi/2`
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) = 4x - 1/x x^2, x in [-2 ,9/2]`
A square piece of tin of side 18 cm is to made into a box without a top by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Show that semi-vertical angle of right circular cone of given surface area and maximum volume is `Sin^(-1) (1/3).`
Find the maximum and minimum of the following functions : y = 5x3 + 2x2 – 3x.
Find the maximum and minimum of the following functions : f(x) = x3 – 9x2 + 24x
Divide the number 30 into two parts such that their product is maximum.
A wire of length 36 metres is bent in the form of a rectangle. Find its dimensions if the area of the rectangle is maximum.
The profit function P(x) of a firm, selling x items per day is given by P(x) = (150 – x)x – 1625 . Find the number of items the firm should manufacture to get maximum profit. Find the maximum profit.
Choose the correct option from the given alternatives :
If f(x) = `(x^2 - 1)/(x^2 + 1)`, for every real x, then the minimum value of f is ______.
Solve the following : A window is in the form of a rectangle surmounted by a semicircle. If the perimeter be 30 m, find the dimensions so that the greatest possible amount of light may be admitted.
Solve the following : Show that the height of a right circular cylinder of greatest volume that can be inscribed in a right circular cone is one-third of that of the cone.
Solve the following : Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is `(2"R")/sqrt(3)`. Also, find the maximum volume.
Determine the maximum and minimum value of the following function.
f(x) = 2x3 – 21x2 + 36x – 20
Determine the maximum and minimum value of the following function.
f(x) = x log x
The function f(x) = x log x is minimum at x = ______.
If f(x) = px5 + qx4 + 5x3 - 10 has local maximum and minimum at x = 1 and x = 3 respectively then (p, q) = ______.
The function y = 1 + sin x is maximum, when x = ______
Find all the points of local maxima and local minima of the function f(x) = `- 3/4 x^4 - 8x^3 - 45/2 x^2 + 105`
Find the points of local maxima, local minima and the points of inflection of the function f(x) = x5 – 5x4 + 5x3 – 1. Also find the corresponding local maximum and local minimum values.
The maximum value of sin x . cos x is ______.
If y `= "ax - b"/(("x" - 1)("x" - 4))` has a turning point P(2, -1), then find the value of a and b respectively.
A function f(x) is maximum at x = a when f'(a) > 0.
If y = alog|x| + bx2 + x has its extremum values at x = –1 and x = 2, then ______.
The maximum value of z = 6x + 8y subject to constraints 2x + y ≤ 30, x + 2y ≤ 24 and x ≥ 0, y ≥ 0 is ______.
The point in the interval [0, 2π], where f(x) = ex sin x has maximum slope, is ______.
If f(x) = `1/(4x^2 + 2x + 1); x ∈ R`, then find the maximum value of f(x).
A running track of 440 m is to be laid out enclosing a football field. The football field is in the shape of a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum,then find the length of its sides. Also calculate the area of the football field.
Sumit has bought a closed cylindrical dustbin. The radius of the dustbin is ‘r' cm and height is 'h’ cm. It has a volume of 20π cm3.
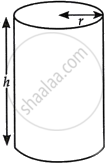
- Express ‘h’ in terms of ‘r’, using the given volume.
- Prove that the total surface area of the dustbin is `2πr^2 + (40π)/r`
- Sumit wants to paint the dustbin. The cost of painting the base and top of the dustbin is ₹ 2 per cm2 and the cost of painting the curved side is ₹ 25 per cm2. Find the total cost in terms of ‘r’, for painting the outer surface of the dustbin including the base and top.
- Calculate the minimum cost for painting the dustbin.
