Advertisements
Advertisements
प्रश्न
The spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find (a) the amplitude and the time period of the motion of the block, (b) the energy stored in the spring when the block passes through the equilibrium position and (c) the kinetic energy of the block at this position.
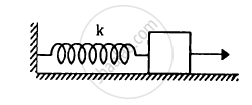
उत्तर
(a) We know-
f = kx
\[\Rightarrow x = \frac{F}{k}\]
\[\text { Acceleration }= \frac{F}{m}\]
Using the relation of time period of S.H.M.,
\[\text { Time period }, T = 2\pi\sqrt{\frac{\text { Displacement } }{\text { Acceleration }}}\]
\[ = 2\pi\sqrt{\frac{\left( \frac{F}{k} \right)}{\left( \frac{F}{m} \right)}} = 2\pi\sqrt{\frac{m}{k}}\]
Amplitude = Maximum displacement \[= \frac{F}{k}\]
When the block passes through the equilibrium position, the energy contained by the spring is given by,
\[E = \frac{1}{2}k x^2 = \frac{1}{2}k \left( \frac{F}{k} \right)^2 = \frac{1}{2}\left( \frac{F^2}{k} \right)\]
(b) At the mean position, potential energy is zero.
Kinetic energy is given by,
\[\frac{1}{2}k x^2 = \frac{1}{2}\frac{F^2}{k}\]
APPEARS IN
संबंधित प्रश्न
A particle executes simple harmonic motion with an amplitude of 10 cm. At what distance from the mean position are the kinetic and potential energies equal?
The maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm/s and 50 cm/s2. Find the position(s) of the particle when the speed is 8 cm/s.
A particle having mass 10 g oscillates according to the equation x = (2.0 cm) sin [(100 s−1)t + π/6]. Find (a) the amplitude, the time period and the spring constant. (c) the position, the velocity and the acceleration at t = 0.
The equation of motion of a particle started at t = 0 is given by x = 5 sin (20t + π/3), where x is in centimetre and t in second. When does the particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?
Repeat the previous exercise if the angle between each pair of springs is 120° initially.
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
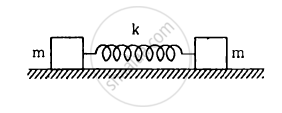
Consider the situation shown in figure . Show that if the blocks are displaced slightly in opposite direction and released, they will execute simple harmonic motion. Calculate the time period.
Discuss in detail the energy in simple harmonic motion.
When a particle executing S.H.M oscillates with a frequency v, then the kinetic energy of the particle?
When the displacement of a particle executing simple harmonic motion is half its amplitude, the ratio of its kinetic energy to potential energy is ______.
If a body is executing simple harmonic motion and its current displacements is `sqrt3/2` times the amplitude from its mean position, then the ratio between potential energy and kinetic energy is:
Motion of an oscillating liquid column in a U-tube is ______.
A body is performing S.H.M. Then its ______.
- average total energy per cycle is equal to its maximum kinetic energy.
- average kinetic energy per cycle is equal to half of its maximum kinetic energy.
- mean velocity over a complete cycle is equal to `2/π` times of its π maximum velocity.
- root mean square velocity is times of its maximum velocity `1/sqrt(2)`.
Displacement versus time curve for a particle executing S.H.M. is shown in figure. Identify the points marked at which (i) velocity of the oscillator is zero, (ii) speed of the oscillator is maximum.

A mass of 2 kg is attached to the spring of spring constant 50 Nm–1. The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
An object of mass 0.5 kg is executing a simple Harmonic motion. Its amplitude is 5 cm and the time period (T) is 0.2 s. What will be the potential energy of the object at an instant t = `T/4` s starting from the mean position? Assume that the initial phase of the oscillation is zero.
