Advertisements
Advertisements
प्रश्न
derive the relation between the change in internal energy (∆U), work is done (W), and heat (Q).
उत्तर
Relation between the change in internal energy (ΔU), work is done (W), and heat (Q):
- When the amount of heat Q is added to the system and the system does not do any work during the process, its internal energy increases by the amount, ΔU = Q.
- When the system does some work to increase its volume, and no heat is added to it while expanding, the system loses energy to its surrounding,s and its internal energy decreases.
∴ ΔU = –W. - As the internal energy can be changed using both ways, we can consider the total change in the internal energy as,
ΔU = Q – W ….(1)
This is the mathematical statement of the first law of thermodynamics.
APPEARS IN
संबंधित प्रश्न
In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3 J is done on the system. If the gas is taken from state A to B via a process in which the net heat absorbed by the system is 9.35 cal, how much is the net work done by the system in the latter case? (Take 1 cal = 4.19 J)
A steam engine delivers 5.4×108 J of work per minute and services 3.6 × 109 J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?
A force F is applied on a block of mass M. The block is displaced through a distance d in the direction of the force. What is the work done by the force on the block? Does the internal energy change because of this work?
The final volume of a system is equal to the initial volume in a certain process. Is the work done by the system necessarily zero? Is it necessarily nonzero?
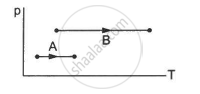
Consider two processes on a system as shown in figure.
The volumes in the initial states are the same in the two processes and the volumes in the final states are also the same. Let ∆W1 and ∆W2 be the work done by the system in the processes A and B respectively.
A gas is contained in a metallic cylinder fitted with a piston. The piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder ______________ .
A 100 kg lock is started with a speed of 2.0 m s−1 on a long, rough belt kept fixed in a horizontal position. The coefficient of kinetic friction between the block and the belt is 0.20. (a) Calculate the change in the internal energy of the block-belt system as the block comes to a stop on the belt. (b) Consider the situation from a frame of reference moving at 2.0 m s−1 along the initial velocity of the block. As seen from this frame, the block is gently put on a moving belt and in due time the block starts moving with the belt at 2.0 m s−1. calculate the increase in the kinetic energy of the block as it stops slipping past the belt. (c) Find the work done in this frame by the external force holding the belt.
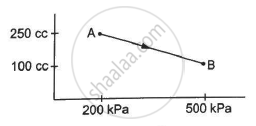
A gas is taken along the path AB as shown in figure. If 70 cal of heat is extracted from the gas in the process, calculate the change in the internal energy of the system.
A gas is initially at a pressure of 100 kPa and its volume is 2.0 m3. Its pressure is kept constant and the volume is changed from 2.0 m3 to 2.5 m3. Its Volume is now kept constant and the pressure is increased from 100 kPa to 200 kPa. The gas is brought back to its initial state, the pressure varying linearly with its volume. (a) Whether the heat is supplied to or extracted from the gas in the complete cycle? (b) How much heat was supplied or extracted?
A system releases 130 kJ of heat while 109 kJ of work is done on the system. Calculate the change in internal energy.
Which of the following system freely allows the exchange of energy and matter with its environment?
What is the energy associated with the random, disordered motion of the molecules of a system called as?
Define heat.
When does a system lose energy to its surroundings and its internal energy decreases?
The internal energy of a system is ______
A thermodynamic system goes from states
(i) P, V to 2P, V (ii) P, V to P, 2V
The work done in the two cases is ____________.
An ideal gas is compressed at a constant temperature. Its internal energy will ____________.
When 1 g of water at 0° C and 1 x 105 N/m2 pressure is converted into ice of volume 1.082 cm3, the external work done will be ____________.
Which of the following represents isothermal process?
In insulated systems, the amount of external work done by the gas is proportional to:
Figure shows the P-V diagram of an ideal gas undergoing a change of state from A to B. Four different parts I, II, III and IV as shown in the figure may lead to the same change of state.

- Change in internal energy is same in IV and III cases, but not in I and II.
- Change in internal energy is same in all the four cases.
- Work done is maximum in case I
- Work done is minimum in case II.
A person of mass 60 kg wants to lose 5kg by going up and down a 10 m high stairs. Assume he burns twice as much fat while going up than coming down. If 1 kg of fat is burnt on expending 7000 kilo calories, how many times must he go up and down to reduce his weight by 5 kg?
An expansion process on a diatomic ideal gas (Cv = 5/2 R), has a linear path between the initial and final coordinates on a pV diagram. The coordinates of the initial state are: the pressure is 300 kPa, the volume is 0.08 m3 and the temperature is 390 K. The final pressure is 90 kPa and the final temperature s 320 K. The change in the internal energy of the gas, in SI units, is closest to:
The internal energy of one mole of argon is ______.
The internal energy of one mole of argon at 300 K is ______. (R = 8.314 J/mol.K)
The molar specific heat of He at constant volume is 12.47 J/mol.K. Two moles of He are heated at constant pressure. So the rise in temperature is 10 K. Find the increase in internal energy of the gas.
A system releases 125 kJ of heat while 104 kJ work is done on the system. Calculate the change in internal energy.
