Advertisements
Advertisements
प्रश्न
Answer the following in one or two sentences.
State the first law of thermodynamics.
उत्तर
According to the first law of thermodynamics, “the total energy of a system and surroundings remains constant when the system changes from an initial state to final state.”
APPEARS IN
संबंधित प्रश्न
An electric heater supplies heat to a system at a rate of 100W. If the system performs work at a rate of 75 Joules per second. At what rate is the internal energy increasing?
Write the mathematical expression of the First Law of Thermodynamics for the Isobaric process.
The first law of thermodynamics is a statement of ____________ .
The internal energy of an ideal gas decreases by the same amount as the work done by the system.
(a) The process must be adiabatic.
b) The process must be isothermal.
(c) The process must be isobaric.
(d) The temperature must decrease.
A thermally insulated, closed copper vessel contains water at 15°C. When the vessel is shaken vigorously for 15 minutes, the temperature rises to 17°C. The mass of the vessel is 100 g and that of the water is 200 g. The specific heat capacities of copper and water are 420 J kg−1 K−1 and 4200 J kg−1 K−1 respectively. Neglect any thermal expansion. (a) How much heat is transferred to the liquid-vessel system? (b) How much work has been done on this system? (c) How much is the increase in internal energy of the system?
Calculate the change in internal energy of a gas kept in a rigid container when 100 J of heat is supplied to it.
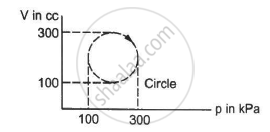
Calculate the heat absorbed by a system in going through the cyclic process shown in figure.
A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
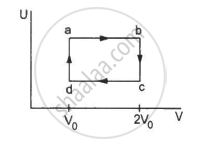
Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
Calculate the increase in the internal energy of 10 g of water when it is heated from 0°C to 100°C and converted into steam at 100 kPa. The density of steam = 0.6 kg m−3. Specific heat capacity of water = 4200 J kg−1 °C−1 and the latent heat of vaporization of water = 2.25 × 10 6J kg−1.
Choose the correct option.
Which of the following is an example of the first law of thermodynamics?
A mixture of hydrogen and oxygen is enclosed in a rigid insulating cylinder. It is ignited by a spark. The temperature and pressure both increase considerably. Assume that the energy supplied by the spark is negligible, what conclusions may be drawn by application of the first law of thermodynamics?
For an Isothermal process
For an Isochoric process
The compressibility of water is 5 × 10-10 m2/N. Pressure of 15 × 106 Pa is applied on 100 ml volume of water. The change in the volume of water is ______.
Two moles of an ideal gas is expanded isothermally and reversibly at 300 K from 1 L to 10 L. The enthalpy change in kJ is ______.
Which of the following are TRUE for a reversible isothermal process?
(i) ∆U = 0
(ii) ∆H = 0
(iii) Q = W
(iv) ∆T = 0
When heat energy of 2000 joules is supplied to a gas at constant pressure 2.1 x 105 N/m2, there is an increase in its volume equal to 2.5 x 10-3 m3. The increase in internal energy of the gas in joules is ____________.
"The mass and energy both are conserved in an isolated system", is the statement of ______.
120 J of heat is added to a gaseous system, whose internal energy change is 60 J, then the amount of external work done is ____________.
For a particular reaction, the system absorbs 8 kJ of heat and does 2.5 kJ of work on its surrounding. What will be the change in internal energy of the system?
The isothermal bulk modulus of a perfect gas at pressure P is numerically equal to ____________.
A sample of gas absorbs 4000 kJ of heat and surrounding does 2000 J of work on sample, what is the value of ΔU?
Change in internal energy, when 4 KJ of work is done on the system and 1 KJ heat is given out by the system, is:
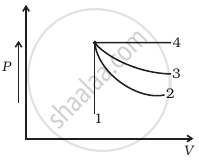
An ideal gas undergoes four different processes from the same initial state (figure). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of 1, 2, 3 and 4 which one is adiabatic.
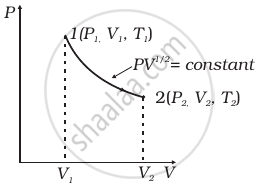
An ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.
- dU = 0
- dQ= 0
- dQ = dU
- dQ = dW
Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in figure.
- Find the work done when the gas is taken from state 1 to state 2.
- What is the ratio of temperature T1/T2, if V2 = 2V1?
- Given the internal energy for one mole of gas at temperature T is (3/2) RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2 = 2V1.
A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure.
A to B : volume constant
B to C : adiabatic
C to D : volume constant
D to A : adiabatic
VC = VD = 2VA = 2VB
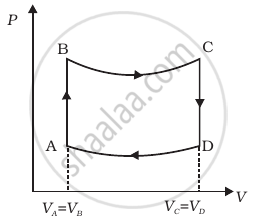
- In which part of the cycle heat is supplied to the engine from outside?
- In which part of the cycle heat is being given to the surrounding by the engine?
- What is the work done by the engine in one cycle? Write your answer in term of PA, PB, VA.
- What is the efficiency of the engine?
(γ = `5/3` for the gas), (Cv = `3/2` R for one mole)
A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in figure. Find heat exchanged by the engine, with the surroundings for each section of the cycle. (Cv = (3/2)R)
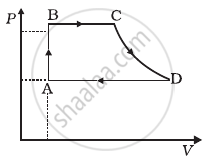
- AB : constant volume
- BC : constant pressure
- CD : adiabatic
- DA : constant pressure
Consider that an ideal gas (n moles) is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
Write the mathematical equation for the first law of thermodynamics for:
Isothermal process
The amount of heat needed to raise the temperature of 4 moles of a rigid diatomic gas from 0°C to 50°C when no work is done is ______.
(R is the universal gas constant.)
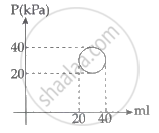
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ______ πJ.
200g water is heated from 40°C to 60°C. Ignoring the slight expansion of water, the change in its internal energy is close to ______.
(Given specific heat of water = 4184 J/kgK)
Mathematical equation of first law of thermodynamics for isochoric process is ______.
One mole of an ideal gas is allowed to expand reversibly and adiabatically from a temperature of 27°C. If the work done during the process is 3 kJ, the final temperature will be equal to ______.
(Cv = 20 JK−1)
Which among the following equations represents the first law of thermodynamics under isobaric conditions?
The amount of work done in increasing the voltage across the plates of capacitor from 5 V to 10 V is W. The work done in increasing it from 10 V to 15 V will be ______.
The V cc volume of gas having `γ = 5/2` is suddenly compressed to `(V/4)` cc. The initial pressure of the gas is p. The final pressure of the gas will be ______.
An ideal gas (γ = 1.5) is expanded adiabatically. How many times has the gas had to be expanded to reduce the root mean square velocity of molecules two times?
104 J of work is done on a certain volume of a gas. If the gas releases 125 kJ of heat, calculate the change in internal energy of the gas.
In an adiabatic process, ______.
If the adiabatic ratio for a gas is 5/3, find the molar specific heat capacity of the gas at (i) constant volume (ii) constant pressure.
In an adiabatic process, W = ______.
For an isothermal and reversible expansion of 0.5 mol of an ideal gas Wmax is - 3.918 kJ. The value of ΔU is ______.
Using the first law of thermodynamics, show that for an ideal gas, the difference between the molar specific heat capacities at constant pressure and at constant volume is equal to the molar gas constant R.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 105 Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 104 Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Taken `γ = 5/3`.
Consider the cyclic process ABCA on a sample of 2.0 mol of an ideal gas as shown in following figure. The temperature of the gas at A and B are 300 K and 500 K respectively. A total of 1200 J heat is withdrawn from the sample in this process. Find the work done by the gas in part BC. (R = 8.3 J/mol K)
Show that the heat absorbed at constant pressure is equal to the change in enthalpy of the system.
Choose the correct relation with reason.
Obtain an expression for the workdone by a gas in an isothermal process.
Calculate work done when 2 moles of ideal gas expands by 5 dm3 isothermally at pressure 1.2 bar.
What is an isothermal process?
