Advertisements
Advertisements
प्रश्न
Expand the expression (1– 2x)5
उत्तर
By using Binomial Theorem, the expression (1– 2x)5 can be expanded as
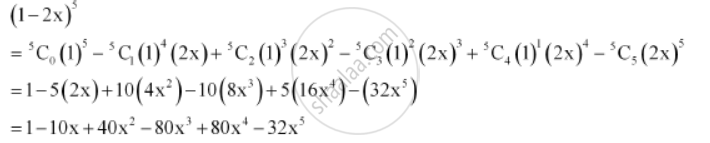
APPEARS IN
संबंधित प्रश्न
Expand the expression: (1– 2x)5
Expand the expression: `(2/x - x/2)^5`
Expand the expression: (2x – 3)6
Expand the expression: `(x + 1/x)^6`
Using Binomial Theorem, evaluate the following:
(96)3
Using binomial theorem, evaluate f the following:
(101)4
Using Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.
Find (x + 1)6 + (x – 1)6. Hence or otherwise evaluate `(sqrt2 + 1)^6 + (sqrt2 -1)^6`
Show that 9n+1 – 8n – 9 is divisible by 64, whenever n is a positive integer.
Prove that `sum_(r-0)^n 3^r ""^nC_r = 4^n`
Find the coefficient of x5 in the product (1 + 2x)6 (1 – x)7 using binomial theorem.
Evaluate `(sqrt3 + sqrt2)^6 - (sqrt3 - sqrt2)^6`
Expand using Binomial Theorem `(1+ x/2 - 2/x)^4, x != 0`
Find the expansion of (3x2 – 2ax + 3a2)3 using binomial theorem.
If n is a positive integer, prove that \[3^{3n} - 26n - 1\] is divisible by 676.
Find the value of (1.01)10 + (1 − 0.01)10 correct to 7 places of decimal.
Evaluate: `(x^2 - sqrt(1 - x^2))^4 + (x^2 + sqrt(1 - x^2))^4`
Find the coefficient of x50 after simplifying and collecting the like terms in the expansion of (1 + x)1000 + x(1 + x)999 + x2(1 + x)998 + ... + x1000 .
The total number of terms in the expansion of (x + a)51 – (x – a)51 after simplification is ______.
The number of terms in the expansion of (a + b + c)n, where n ∈ N is ______.
If z = `sqrt(3)/2 + i^5/2 + sqrt(3)/2 - i^5/2`, then ______.
Find the coefficient of x in the expansion of (1 – 3x + 7x2)(1 – x)16.
Find the coefficient of x15 in the expansion of (x – x2)10.
Find the sixth term of the expansion `(y^(1/2) + x^(1/3))^"n"`, if the binomial coefficient of the third term from the end is 45.
Find the coefficient of x4 in the expansion of (1 + x + x2 + x3)11.
The total number of terms in the expansion of (x + a)100 + (x – a)100 after simplification is ______.
The number of terms in the expansion of (x + y + z)n ______.
The coefficient of a–6b4 in the expansion of `(1/a - (2b)/3)^10` is ______.
Let the coefficients of x–1 and x–3 in the expansion of `(2x^(1/5) - 1/x^(1/5))^15`, x > 0, be m and n respectively. If r is a positive integer such that mn2 = 15Cr, 2r, then the value of r is equal to ______.
The sum of the last eight coefficients in the expansion of (1 + x)16 is equal to ______.
If the coefficients of (2r + 4)th, (r – 2)th terms in the expansion of (1 + x)18 are equal, then r is ______.
Let `(5 + 2sqrt(6))^n` = p + f where n∈N and p∈N and 0 < f < 1 then the value of f2 – f + pf – p is ______.
The positive integer just greater than (1 + 0.0001)10000 is ______.
