Advertisements
Advertisements
प्रश्न
If a parabolic reflector is 20 cm in diameter and 5 cm deep, find its focus.
उत्तर
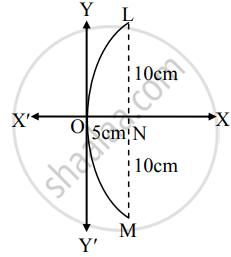
Let LOM be the parabolic reflector such that LM is the diameter and ON is its depth.
It is given that ON = 5 cm and LM = 20 cm.
∴ LN = 10 cm
Taking O as the origin, ON along X-axis and a line through O ⊥ ON as Y-axis.
Let the equation of the reflector be
y2 = 4ax ...(i)
The point L has the co-ordinates (5, 10) and lies on parabola given by (i).
Substituting x = 5 and y = 10 in (i), we get
102 = 4a (5)
∴ 100 = 20a
∴ a = 5
Focus is at (a, 0), i.e., (5, 0).
APPEARS IN
संबंधित प्रश्न
Find co-ordinate of focus, equation of directrix, length of latus rectum and the co-ordinate of end points of latus rectum of the parabola:
3x2 = 8y
Find co-ordinate of focus, equation of directrix, length of latus rectum and the co-ordinate of end points of latus rectum of the parabola:
x2 = –8y
Find co-ordinate of focus, equation of directrix, length of latus rectum and the co-ordinate of end points of latus rectum of the parabola:
3y2 = –16x
Find the equation of the parabola with vertex at the origin, axis along X-axis and passing through the point (3, 4)
Find the equation of the parabola with vertex at the origin, axis along X-axis and passing through the point (1, –6)
Find coordinates of the point on the parabola. Also, find focal distance.
2y2 = 7x whose parameter is –2
Find length of latus rectum of the parabola y2 = 4ax passing through the point (2, –6)
Find coordinate of focus, vertex and equation of directrix and the axis of the parabola y = x2 – 2x + 3
Find the equation of tangent to the parabola y2 = 36x from the point (2, 9)
If the tangent drawn from the point (–6, 9) to the parabola y2 = kx are perpendicular to each other, find k
Find the equation of common tangent to the parabola y2 = 4x and x2 = 32y
Find the equation of the locus of a point, the tangents from which to the parabola y2 = 18x are such that some of their slopes is –3
Select the correct option from the given alternatives:
If the focus of the parabola is (0, –3) its directrix is y = 3 then its equation is
Select the correct option from the given alternatives:
Equation of the parabola with vertex at the origin and directrix x + 8 = 0 is __________
Select the correct option from the given alternatives:
If the parabola y2 = 4ax passes through (3, 2) then the length of its latus rectum is ________
Answer the following:
Find the co-ordinates of a point of the parabola y2 = 8x having focal distance 10
Answer the following:
Find the equations of the tangents to the parabola y2 = 9x through the point (4, 10).
Answer the following:
Show that the two tangents drawn to the parabola y2 = 24x from the point (−6, 9) are at the right angle
Answer the following:
A line touches the circle x2 + y2 = 2 and the parabola y2 = 8x. Show that its equation is y = ± (x + 2).
Answer the following:
The slopes of the tangents drawn from P to the parabola y2 = 4ax are m1 and m2, show that m1 − m2 = k, where k is a constant.
Answer the following:
The slopes of the tangents drawn from P to the parabola y2 = 4ax are m1 and m2, show that `("m"_1 /"m"_2)` = k, where k is a constant.
Answer the following:
The tangent at point P on the parabola y2 = 4ax meets the y-axis in Q. If S is the focus, show that SP subtends a right angle at Q
Answer the following:
Find the
(i) lengths of the principal axes
(ii) co-ordinates of the foci
(iii) equations of directrices
(iv) length of the latus rectum
(v) Distance between foci
(vi) distance between directrices of the curve
16x2 + 25y2 = 400
Answer the following:
Find the
(i) lengths of the principal axes
(ii) co-ordinates of the foci
(iii) equations of directrices
(iv) length of the latus rectum
(v) Distance between foci
(vi) distance between directrices of the curve
`x^2/144 - y^2/25` = 1
The equation of the directrix of the parabola 3x2 = 16y is ________.
The locus of the mid-point of the line segment joining the focus of the parabola y2 = 4ax to a moving point of the parabola, is another parabola whose directrix is ______.
If a line along a chord of the circle 4x2 + 4y2 + 120x + 675 = 0, passes through the point (–30, 0) and is tangent to the parabola y2 = 30x, then the length of this chord is ______.
If the line `y - sqrt(3)x + 3` = 0 cuts the parabola y2 = x + 2 at A and B, then PA. PB is equal to `("where coordinates of P are" (sqrt(3), 0))` ______.
If the normal at the point (1, 2) on the parabola y2 = 4x meets the parabola again at the point (t2, 2t), then t is equal to ______.
The centre of the circle passing through the point (0, 1) and touching the parabola y = x2 at the point (2, 4) is ______.
The equation to the line touching both the parabolas y2 = 4x and x2 = –32y is ______.
If the vertex = (2, 0) and the extremities of the latus rectum are (3, 2) and (3, –2) then the equation of the parabola is ______.
Two parabolas with a common vertex and with axes along x-axis and y-axis, respectively, intersect each other in the first quadrant. if the length of the latus rectum of each parabola is 3, then the equation of the common tangent to the two parabolas is ______.
If vertex of a parabola is (2, –1) and the equation of its directrix is 4x – 3y = 21, then the length of its latus rectum is ______.
