Advertisements
Advertisements
प्रश्न
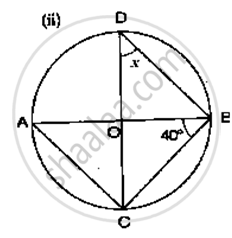
If O is the centre of the circle, find the value of x in the following figure:
उत्तर
We have
∠ABC = 40°
∠ACB = 90°
In ∠ABC, by angle sum property
∠CAB + ∠ACB + ∠ABC = 180°
⇒ ∠CAB + 90° + 40° = 180°
⇒ ∠CAB = 180° - 90°
⇒ ∠CAB = 50°
Now,
⇒COB = ∠CAB
⇒x = 50°
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
If O is the centre of the circle, find the value of x in the following figure

O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
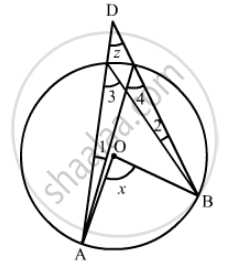
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
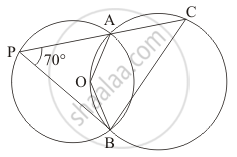
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
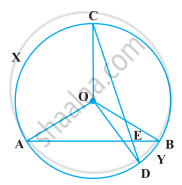
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).