Advertisements
Advertisements
प्रश्न
If sin A = `1/3`, sin B = `1/4` then find the value of sin (A + B) where A and B are acute angles.
उत्तर
Since A and B are acute angles, all the ratios are positive.
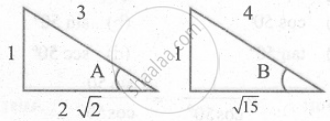
sin A = `1/3`; sin B = `1/4`; cos A = `(2sqrt2)/3`; cos B = `sqrt15/4`
∴ sin (A + B) = sin A cos B + cos A sin B
`= 1/3 * sqrt15/4 + (2sqrt2)/3 * 1/4`
`= sqrt15/12 + (2sqrt2)/12`
`= (sqrt15 + 2sqrt2)/12`
APPEARS IN
संबंधित प्रश्न
Find the value of the following:
cosec 15º
Find the value of the following:
sin 76° cos 16° – cos 76° sin 16°
Find the value of the following:
cos2 15° – sin2 15°
If cos A = `13/14` and cos B = `1/7` where A, B are acute angles prove that A – B = `pi/3`
If A + B = 45°, prove that (1 + tan A) (1 + tan B) = 2 and hence deduce the value of tan 22`1/2`.
Prove that:
sin(A + 60°) + sin(A – 60°) = sin A.
Prove that:
tan 4A tan 3A tan A + tan 3A + tan A – tan 4A = 0
If sin α + sin β = a and cos α + cos β = b, then prove that cos(α – β) = `(a^2 + b^2 - 2)/2`
If tan α = `1/7`, sin β = `1/sqrt10`. Prove that α + 2β = `pi/4` where 0 < α < `pi/2` and 0 < β < `pi/2`.
If p sec 50° = tan 50° then p is:
