Advertisements
Advertisements
प्रश्न
On the basis of Huygens' wave theory of light prove that velocity of light in a rarer medium is greater than velocity of light in a denser medium.
उत्तर

XY : plane refracting surface
AB : incident plane wavefront
B1R : refracted wavefront
AA1 , BB1 : incident rays
A1R , B1R1 : refracted rays
∠ AA1M = ∠ BB1M1 = ∠ i : angle of incidence
∠ RA1N = ∠ R1B1N1 = ∠ r : angle of refraction
- Let XY be the plane refracting surface separating two media rarer and denser of refractive indices μ1 and μ2 respectively.
- A plane wavefront AB is advancing obliquely towards XY from rarer medium. It is bounded by rays AA1 and BB1 which are incident rays.
- When 'A' reaches at 'A1' then 'B' will be at 'P' . It still has to cover distance PB1 to reach XY.
- According to Huygens' principle , secondary wavelets will originate from A1 and it will spread over a hemisphere in denser medium.
- All the rays between AA1 and BB1 will reach XY and spread over the hemispheres of increasing radii in denser medium. The surface of tangency of all such hemisphere is RB1 . This gives rise to refracted wavefront B1R in denser medium.
- A1R and B1R are refracted rays.
- Let c1 and c2 be the velocities of light in rarer and denser medium respectively.
- At any instant of time 't' , distance covered by incident wavelength from P to B1 = PB1 = c1t
Distance covered by secondary wave from A1 to R = A1R =c2t . - From above figure ,
∠ AA1M + ∠ MA1P = 90° .....(i) and
∠ MA1P + ∠ PA1B1 = 90° ...........(ii)
From equation (i) and (ii) , we have,
∠ AA1M = ∠ PA1B1 = 90° - Similarly ,
∠NA1R = ∠ N1B1R1 = r
We have,
∠ N1B1R1 + ∠ A1B1R = 90° .........(iii)
and
∠ N1B1R1 + ∠ A1B1R = 90° .........(iv)
From equations (iii) and (iv) , we have,
∠ N1B1R1 + ∠ A1B1R = r - In Δ A1PB1 ,
sin i = `"PB"_1/("A"_1"B"_1) = ("c"_1"t")/("A"_1"B"_1)` ........(v) - In Δ A1RB1 ,
sin r = `("A"_1"R")/("A"_1"B"_1) = ("c"_2"t")/("A"_1"B"_1)` ............(vi) - Dividing equation (v) bt (vi), we have
`("sin" "i")/("sin""r") = ((c_1t) / (A_1B_1))/((c_2t)/(A_1B_1))`
`therefore ("sin" "i")/("sin""r") = c_1/c_2` .....(vii)
Also `c_1/c_2 = mu_2/mu_1 = 1 mu_2` .....(viii)
where 1μ2 = R.I. of denser medium w.r.t rarer medium. - From above figure ,
∠ i > ∠ r
∴ sin i > sin r
∴ `("sin" "i")/("sin" "r") > 1`
`therefore mu_2/mu_1 > 1` .........(ix)
Since , `c_1/c_2 = mu_2/mu_1` ..........[From ix]
`therefore c_1/c_2 > 1`
`therefore c_1 > c_2`
Hence , velocity of light in rarer medium is greater than veocity in denser medium.
APPEARS IN
संबंधित प्रश्न
Using Huygens's construction of secondary wavelets explain how a diffraction pattern is obtained on a screen due to a narrow slit on which a monochromatic beam of light is incident normally.
Explain the construction of plane wavefront using Huygens’ principle.
You have learnt in the text how Huygens’ principle leads to the laws of reflection and refraction. Use the same principle to deduce directly that a point object placed in front of a plane mirror produces a virtual image whose distance from the mirror is equal to the object distance from the mirror.
State Huygen's principle.
Consider a plane wave front incident on a thin convex lens. Draw a proper diagram to show how the incident wave front traverses through the lens and after refraction focusses on the focal point of the lens, giving the shape of the emergent wave front.
The refractive indices of water and diamond are `4/3` and 2.42 respectively. Find the speed of light in water and diamond. (c = 3x108 m/s)
Using Huygens’ principle, verify the laws of reflection at a plane surface.
Using this principle draw a diagram to show how a plane wave front incident at the interface of the two media gets refracted when it propagates from a rarer to a denser medium. Hence verify Snell's law of refraction.
Use Huygens’s principle to explain the formation of diffraction pattern due to a single slit illuminated by a monochromatic source of light.
When the width of the slit is made double the original width, how would this affect the size and intensity of the central diffraction band?
Huygens' principle of secondary wavelets may be used to
(a) find the velocity of light in vacuum
(b) explain the particle behaviour of light
(c) find the new position of a wavefront
(d) explain Snell's Law
Derive the law of reflection using Huygen’s Wave Theory.
Define the term wavefront. Using Huygen’s wave theory, verify the law of reflection.
Answer the following question.
Define the term wavefront. Using Huygen's wave theory, verify the law of reflection.
Define the term 'wavefront of light'. A plane wavefront AB propagating from a denser medium (1) into a rarer medium (2) is incident of the surface P1P2 separating the two media as shown in fig.
Using Huygen's principle, draw the secondary wavelets and obtain the refracted wavefront in the diagram.
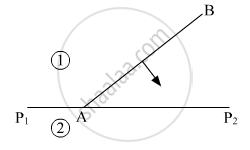
According to Huygen's construction, relation between old and new wavefront is ______.
Relation between ray and wavefront is ______.
What is the phase difference between any two points lying on the same?
Huygen's conception of secondary waves ______.
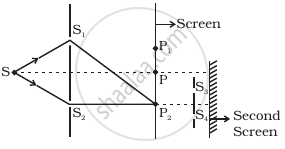
Figure shows a standard two slit arrangement with slits S1, S2, P1, P2 are the two minima points on either side of P (Figure). At P2 on the screen, there is a hole and behind P2 is a second 2-slit arrangement with slits S3, S4 and a second screen behind them.
Consider a point at the focal point of a convergent lens. Another convergent lens of short focal length is placed on the other side. What is the nature of the wavefronts emerging from the final image?
What is the shape of the wavefront on earth for sunlight?
Using Huygen's wave theory of light, show that the angle of incidence is equal to the angle of reflection. Draw a neat and labelled diagram.
Represent diagrammatically how the incident planar wavefronts of wavelength λ pass through an aperture of size d, when d is approximately equal to λ.
