Advertisements
Advertisements
प्रश्न
Why is the surface tension of paints and lubricating oils kept low?
उत्तर
The surface tension of paints and lubricating oils is kept low so that they can spread over large areas easily and quickly.
संबंधित प्रश्न
The surface tension of water at 0°C is 75.5 dyne/cm. Calculate surface tension of water at 25°C.
(α for water = 2.7×10-3/°C)
Derive an expression for excess pressure inside a drop of liquid.
The surface tension of water at 0ºc is 75·5 dyne/cm. Find surface tension of water at 25°C. [ α for water = 0·0021/°C ]
Explain why The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
Explain why Water with detergent dissolved in it should have small angles of contact.
Fill in the blanks using the word(s) from the list appended with each statement
Surface tension of liquids generally . . . with temperatures (increases / decreases)
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass
of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a
vertical axis, calculate tension in the string (g = 9.8 m/s2)
A big drop of radius R is formed from 1000 droplets of water. The radius of a droplet will be _______
A) 10 R
B) R/10
C) R/100
D) R/1000
State any two characteristics of the angle of contact
The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary?
It is said that a liquid rises or is depressed in capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero?
A uniform vertical tube of circular cross section contains a liquid. The contact angle is 90°. Consider a diameter of the tube lying in the surface of the liquid. The surface to the right of this diameter pulls the surface on the left of it. What keeps the surface on the left in equilibrium?
The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to excess pressure inside a bubble balanced by the force due to the surface tension?
When the size of a soap bubble is increased by pushing more air in it, the surface area increases. Does it mean that the average separation between the surface molecules is increased?
By a surface of a liquid we mean
When water droplets merge to form a bigger drop
If two soap bubbles of different radii are connected by a tube,
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
The rise of a liquid in a capillary tube depends on
(a) the material
(b) the length
(c) the outer radius
(d) the inner radius of the tube
A liquid is contained in a vertical tube of semicircular cross section. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio
When a capillary tube is dipped into a liquid, the liquid neither rises nor falls in the capillary.
(a) The surface tension of the liquid must be zero.
(b) The contact angle must be 90°.
(c) The surface tension may be zero.
(d) The contact angle may be 90°.
A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass = 135° and surface tension of mercury = 0.465 N m−1. Density of mercury = 13600 kg m−3.
Find the surface energy of water kept in a cylindrical vessel of radius 6.0 cm. Surface tension of water = 0.075 J m−2.
A drop of mercury of radius 2 mm is split into 8 identical droplets. Find the increase in surface energy. Surface tension of mercury = 0.465 J m−2.
Two large glass plates are placed vertically and parallel to each other inside a tank of water with separation between the plates equal to 1 mm. Find the rise of water in the space between the plates. Surface tension of water = 0.075 Nm−1.
A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension the the thread. Surface tension of soap solution = 0.030 N m−1.
A cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
A hollow spherical body of inner and outer radii 6 cm and 8 cm respectively floats half-submerged in water. Find the density of the material of the sphere.
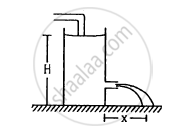
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
Explain the capillary action.
Insect moves over the surface of water because of ______.
The surface tension of a liquid at critical temperature is ______
Explain the phenomena of surface tension on the basis of molecular theory.
Describe an experiment to prove that friction depends on the nature of a surface.
Explain elasticity using intermolecular forces.
Mention the S.I unit and dimension of surface tension.
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
A large number of liquid drops each of radius 'r' coalesce to form a big drop of radius 'R'. The energy released in the process in converted into kinetic energy of the big drop. The speed of the big drop is ______. (T = surface tension of liquid, p = density of liquid)
Soap solution is used for cleaning dirty clothes because ______.
The wear and tear in the machine part is due to ______.
What is surface tension? Explain the applications of surface tension.
For a surface molecule ______.
- the net force on it is zero.
- there is a net downward force.
- the potential energy is less than that of a molecule inside.
- the potential energy is more than that of a molecule inside.
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10–3 Nm–1.
This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg–1, the mechanical equivalent of heat J = 4.2 J cal–1, density of water ρw = 103 kg l–1, Avagadro’s No NA = 6.0 × 1026 k mole–1 and the molecular weight of water MA = 18 kg for 1 k mole.
- Estimate the energy required for one molecule of water to evaporate.
- Show that the inter–molecular distance for water is `d = [M_A/N_A xx 1/ρ_w]^(1/3)` and find its value.
- 1 g of water in the vapor state at 1 atm occupies 1601 cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
- During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d ′. Estimate the value of F.
- Calculate F/d, which is a measure of the surface tension.
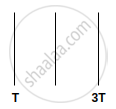
We have three identical perfectly black plates. The temperatures of first and third plate is T and 3T. What is the temperature of second plate if system is in equilibrium?
A drop of water and a soap bubble have the same radii. Surface tension of soap solution is half of that of water. The ratio of excess pressure inside the drop and bubble is ______.
In a U-tube, the radii of two columns are respectively r1 and r2. When a liquid of density ρ(θ = 0°) is filled in it, a level difference of h is observed on two arms, then the surface tension of the liquid is ______.
The excess pressure inside a liquid drop is 500 Nm-2. If the radius of the drop is 2 mm, the surface tension of the liquid is x × 10-3 Nm-1. The value of x is ______.
In most liquids, with the rise in temperature, the surface tension of a liquid ______.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
