Advertisements
Advertisements
सिद्ध करा 'चक्रीय चौकोनाचे संमुख कोन परस्परांचे पूरककोन असतात.'
Concept: चक्रीय चौकोनाचे प्रमेय
खालील बिंदू एकरेषीय आहेत की नाहीत हे ठरवा.
A(1, −3), B(2, −5), C(−4, 7)
Concept: अंतराचे सूत्र (Distance Formula)
जर sinθ = `11/61`, तर नित्यसमानतेचा उपयोग करून cosθ ची किंमत काढा.
Concept: त्रिकोणमितीय नित्यसमानता
समलंब चौकोन ABCD मध्ये, बाजू AB || बाजू PQ || बाजू DC, जर AP = 15, PD = 12, QC = 14 तर BQ काढा.

Concept: तीन समांतर रेषा व त्यांच्या छेदिका यांचा गुणधर्म
ΔLMN ~ ΔPQR, 9 × A(ΔPQR) = 16 × A(ΔLMN) जर QR = 20 तर MN काढा.
Concept: समरूप त्रिकोणांच्या क्षेत्रफळांचे प्रमेय
जर ΔABC व ΔPQR मध्ये एका एकास एक संगतीत `"AB"/"QR" = "BC"/"PR" = "CA"/"PQ"` तर खालीलपैकी सत्य विधान कोणते?

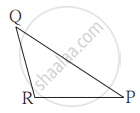
Concept: त्रिकोणांच्या समरूपतेच्या कसोट्या
∆ABC मध्ये, B-D-C आणि BD = 7, BC = 20, तर खालील गुणोत्तर काढा.
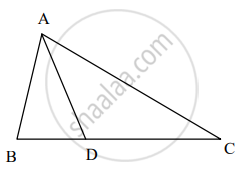
`(A(∆ABD))/(A(∆ABC))`
Concept: दोन त्रिकोणांच्या क्षेत्रफळांच्या गुणोत्तराचे गुणधर्म
जर ΔABC ∼ ΔDEF आणि ∠A = 48°, तर ∠D = ______.
Concept: त्रिकोणांच्या समरूपतेच्या कसोट्या
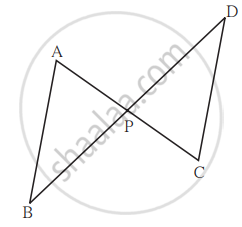
वरील आकृतीत रेख AC आणि रेख BD परस्परांना P बिंदूत छेदतात. जर `"AP"/"CP" = "BP"/"DP"` तर ΔABP ∼ ΔCDP दाखवण्यासाठी खालील कृती पूर्ण करा.
कृती: ΔABP व ΔCDP मध्ये
`"AP"/"CP" = "BP"/"DP" ....square`
∠APB ≅ `square` ...... विरुद्ध कोन
∴ `square` ∼ ΔCDP ....... समरूपतेची `square` कसोटी.
Concept: त्रिकोणांच्या समरूपतेच्या कसोट्या
जर ΔABC ∼ ΔPQR, AB : PQ = 4 : 5 आणि A(ΔPQR) = 125 सेमी2 असेल, तर A(ΔABC) काढा.
Concept: समरूप त्रिकोणांच्या क्षेत्रफळांचे प्रमेय

वरील आकृतीत, ΔABC मध्ये रेख XY || बाजू AC, जर 2AX = 3BX आणि XY = 9, तर AC ची किंमत काढा.
Concept: त्रिकोणांच्या समरूपतेच्या कसोट्या
ΔABC ∼ ΔPQR, ΔABC मध्ये AB = 5.4 सेमी, BC = 4.2 सेमी, AC = 6.0 सेमी, AB : PQ = 3 : 2, तर ΔABC आणि ΔPQR ची रचना करा.
Concept: समरूप त्रिकोणांच्या क्षेत्रफळांचे प्रमेय

Concept: त्रिकोणांच्या समरूपतेच्या कसोट्या
जर ΔABC ∼ ΔPQR आणि `("A"(Delta"ABC"))/(A(Delta"PQR")) = 16/25` तर AB : PQ किती?
Concept: समरूप त्रिकोणांच्या क्षेत्रफळांचे प्रमेय
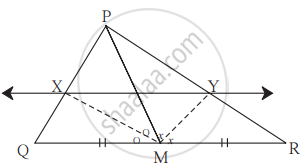
ΔPQR मध्ये रेख PM ही मध्यगा आहे. ∠PMQ व ∠PMR चे दुभाजक बाजू PQ व बाजू PR ला अनुक्रमे X आणि Y बिंदूत छेदतात. तर XY || QR सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
उकल:
ΔPMQ मध्ये,
किरण MX हा ∠PMQ चा कोनदुभाजक आहे.
∴ `"MP"/"MQ" = square/square` .............(I) (कोनदुभाजकाचे प्रमेय)
ΔPMR मध्ये किरण MY हा ∠PMR चा कोनदुभाजक आहे.
∴ `"MP"/"MR" = square/square` .............(II) (कोनदुभाजकाचे प्रमेय)
परंतु `"MP"/"MQ" = "MP"/"MR"` ................(III) (M हा QR चा मध्यबिंदू आहे म्हणजेच MQ = MR)
∴ `"PX"/square = square/"YR"` ............(विधान (I), (II) व (III) वरून)
∴ XY || QR ...........(प्रमाणाच्या मूलभूत प्रमेयाचा व्यत्यास)
Concept: त्रिकोणाच्या कोनदुभाजकाचे प्रमेय
ΔABC मध्ये रेख DE || बाजू BC. जर 2A(ΔADE) = A(⬜ DBCE), तर AB : AD आणि BC = `sqrt3` DE दाखवा.
Concept: समरूप त्रिकोणांच्या क्षेत्रफळांचे प्रमेय
समलंब चौकोन ABCD मध्ये बाजू AB || बाजू CD चौकोनाचे कर्ण हे एकमेकांना बिंदू P मध्ये छेदतात.
त्यावरून खालील प्रश्नांची उत्तरे लिहा:
- वरील दिलेल्या माहितीवरून आकृती काढा.
- व्युत्क्रम कोन व विरुद्ध कोनांची प्रत्येकी एक जोडी लिहा.
- समरूप त्रिकोणांची नावे समरूपतेच्या कसोटीसह लिहा.
Concept: त्रिकोणांच्या समरूपतेच्या कसोट्या
जर ∆ABC ~ ∆PQR आणि AB : PQ = 2 : 3, तर `("A" (∆"ABC"))/("A"(∆"PQR"))` ची किंमत काढा.
Concept: समरूप त्रिकोणांच्या क्षेत्रफळांचे प्रमेय
"त्रिकोणाच्या एका बाजूला समांतर असणारी रेषा त्याच्या उरलेल्या बाजूंना भिन्न बिंदूत छेदत असेल, तर ती रेषा त्या बाजूंना एकाच प्रमाणात विभागते.” हे सिद्ध करा.
Concept: प्रमाणाचे मूलभूत प्रमेय

ΔABC मध्ये, किरण BD हा ∠ABC चा दुभाजक आहे. A - D - C, रेख DE || बाजू BC, A - E - B, तर `("AB")/("BC") = ("AE")/("EB")` हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा:
सिद्धता:
ΔABC मध्ये, किरण BD हा ∠B चा दुभाजक आहे.
∴ `square/("BC") = ("AD")/("DC")` ......(I) (`square`)
ΔABC मध्ये, DE || BC
∴ `(square)/("EB") = ("AD")/("DC")` ....(II) (`square`)
∴ `("AB")/square = square/("EB")` [(I) व (II)वरून]
Concept: त्रिकोणाच्या कोनदुभाजकाचे प्रमेय
