Advertisements
Advertisements
Question
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has no girls
Solution
We have 4 girls and 7 boys and a team of 5 members is to be selected.
If no girl is selected, then all the 5 members are to be selected out of 7 boys
i.e. 7C5 = `(7!)/(5!2!)`
= `(7 xx 6.51)/(51 xx 2)`
= 21 ways
Hence the required number of ways are 21 ways.
APPEARS IN
RELATED QUESTIONS
In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?
How many words, with or without meaning, can be formed using all the letters of the word EQUATION at a time so that the vowels and consonants occur together?
A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of:
(i) exactly 3 girls?
(ii) atleast 3 girls?
(iii) atmost 3 girls?
The English alphabet has 5 vowels and 21 consonants. How many words with two different vowels and 2 different consonants can be formed from the alphabet?
In a class there are 27 boys and 14 girls. The teacher wants to select 1 boy and 1 girl to represent the class in a function. In how many ways can the teacher make this selection?
How many different five-digit number licence plates can be made if
first digit cannot be zero and the repetition of digits is not allowed,
In how many ways can six persons be seated in a row?
If 2nC3 : nC2 = 44 : 3, find n.
There are 10 professors and 20 students out of whom a committee of 2 professors and 3 students is to be formed. Find the number of ways in which this can be done. Further find in how many of these committees:
a particular student is excluded.
From a class of 12 boys and 10 girls, 10 students are to be chosen for a competition; at least including 4 boys and 4 girls. The 2 girls who won the prizes last year should be included. In how many ways can the selection be made?
Find the number of diagonals of (ii) a polygon of 16 sides.
A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of: exactly 3 girls?
A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of: atmost 3 girls?
Out of 18 points in a plane, no three are in the same straight line except five points which are collinear. How many (ii) triangles can be formed by joining them?
How many words can be formed by taking 4 letters at a time from the letters of the word 'MORADABAD'?
If 20Cr = 20Cr + 4 , then rC3 is equal to
If nC12 = nC8 , then n =
Find n if `""^6"P"_2 = "n" ""^6"C"_2`
There are 8 doctors and 4 lawyers in a panel. Find the number of ways for selecting a team of 6 if at least one doctor must be in the team.
Find the value of 15C4 + 15C5
In how many ways a committee consisting of 3 men and 2 women, can be chosen from 7 men and 5 women?
A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected from the lot.
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has at least three girls.
The number of ways in which a team of eleven players can be selected from 22 players always including 2 of them and excluding 4 of them is ______.
The number of ways in which we can choose a committee from four men and six women so that the committee includes at least two men and exactly twice as many women as men is ______.
Given 5 different green dyes, four different blue dyes and three different red dyes, the number of combinations of dyes which can be chosen taking at least one green and one blue dye is ______.
A badminton club has 10 couples as members. They meet to organise a mixed double match. If each wife refers to p artner as well as oppose her husband in the match, then the number of different ways can the match off will be ______.
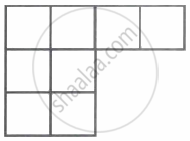
The no. of different ways, the letters of the word KUMARI can be placed in the 8 boxes of the given figure so that no row remains empty will be ______.
The number of numbers between 2,000 and 5,000 that can be formed with the digits 0, 1, 2, 3, 4, (repetition of digits is not allowed) and are multiple of 3 is?
From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on the shelf so that the dictionary is always in the middle. Then, the number of such arrangements is ______.
