Advertisements
Advertisements
Question
A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of:
(i) exactly 3 girls?
(ii) atleast 3 girls?
(iii) atmost 3 girls?
Solution
A committee of 7 has to be formed from 9 boys and 4 girls.
i) Since exactly 3 girls are to be there in every committee, each committee must consist of (7 – 3) = 4 boys only.
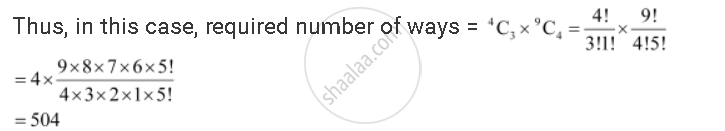
(ii) Since at least 3 girls are to be there in every committee, the committee can consist of
(a) 3 girls and 4 boys or (b) 4 girls and 3 boys
3 girls and 4 boys can be selected in `""^4C_3 xx ""^9C_4` ways.
4 girls and 3 boys can be selected in `""^4C_4 xx ""^9C_3` ways.

(iii) Since atmost 3 girls are to be there in every committee, the committee can consist of
(a) 3 girls and 4 boys (b) 2 girls and 5 boys
(c) 1 girl and 6 boys (d) No girl and 7 boys

APPEARS IN
RELATED QUESTIONS
Determine n if `""^(2n)C_3 : ""^nC_3 = 12 : 1`
In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?
In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?
A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
How many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER?
It is required to seat 5 men and 4 women in a row so that the women occupy the even places. How many such arrangements are possible?
From a class of 25 students, 10 are to be chosen for an excursion party. There are 3 students who decide that either all of them will join or none of them will join. In how many ways can the excursion party be chosen?
Compute:
(i)\[\frac{30!}{28!}\]
A mint prepares metallic calendars specifying months, dates and days in the form of monthly sheets (one plate for each month). How many types of calendars should it prepare to serve for all the possibilities in future years?
How many A.P.'s with 10 terms are there whose first term is in the set {1, 2, 3} and whose common difference is in the set {1, 2, 3, 4, 5}?
How many different five-digit number licence plates can be made if
first digit cannot be zero and the repetition of digits is not allowed,
In how many ways can six persons be seated in a row?
Serial numbers for an item produced in a factory are to be made using two letters followed by four digits (0 to 9). If the letters are to be taken from six letters of English alphabet without repetition and the digits are also not repeated in a serial number, how many serial numbers are possible?
Evaluate the following:
35C35
If nC4 = nC6, find 12Cn.
In how many ways can a football team of 11 players be selected from 16 players? How many of these will
exclude 2 particular players?
Find the number of diagonals of , 1.a hexagon
Find the number of (i) diagonals
Find the number of (ii) triangles
In an examination, a question paper consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions?
A parallelogram is cut by two sets of m lines parallel to its sides. Find the number of parallelograms thus formed.
Find the number of combinations and permutations of 4 letters taken from the word 'EXAMINATION'.
A tea party is arranged for 16 persons along two sides of a long table with 8 chairs on each side. Four persons wish to sit on one particular side and two on the other side. In how many ways can they be seated?
If C (n, 12) = C (n, 8), then C (22, n) is equal to
If\[\ ^{( a^2 - a)}{}{C}_2 = \ ^{( a^2 - a)}{}{C}_4\] , then a =
If 43Cr − 6 = 43C3r + 1 , then the value of r is
In a small village, there are 87 families, of which 52 families have atmost 2 children. In a rural development programme 20 families are to be chosen for assistance, of which atleast 18 families must have at most 2 children. In how many ways can the choice be made?
The straight lines l1, l2 and l3 are parallel and lie in the same plane. A total numbers of m points are taken on l1; n points on l2, k points on l3. The maximum number of triangles formed with vertices at these points are ______.
If nC12 = nC8, then n is equal to ______.
In a football championship, 153 matches were played, Every two teams played one match with each other. The number of teams, participating in the championship is ______.
A box contains 2 white balls, 3 black balls and 4 red balls. The number of ways three balls be drawn from the box if at least one black ball is to be included in the draw is ______.
All possible numbers are formed using the digits 1, 1, 2, 2, 2, 2, 3, 4, 4 taken all at a time. The number of such numbers in which the odd digits occupy even places is ______.
There are 12 balls numbered from 1 to 12. The number of ways in which they can be used to fill 8 places in a row so that the balls are with numbers in ascending or descending order is equal to ______.
There are (n + 1) white and (n + 1) black balls each set numbered 1 to (n + 1). The number of ways in which the balls can be arranged in row so that the adjacent balls are of different colours is ______.
