Advertisements
Advertisements
Question
If 43Cr − 6 = 43C3r + 1 , then the value of r is
Options
12
8
6
10
14
Solution
12
\[ \Rightarrow 4r = 48\]
\[ \Rightarrow r = 12\]
APPEARS IN
RELATED QUESTIONS
If nC8 = nC2, find nC2.
In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?
In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?
How many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER?
From a class of 25 students, 10 are to be chosen for an excursion party. There are 3 students who decide that either all of them will join or none of them will join. In how many ways can the excursion party be chosen?
Prove that
In a class there are 27 boys and 14 girls. The teacher wants to select 1 boy and 1 girl to represent the class in a function. In how many ways can the teacher make this selection?
There are 6 multiple choice questions in an examination. How many sequences of answers are possible, if the first three questions have 4 choices each and the next three have 2 each?
A team consists of 6 boys and 4 girls and other has 5 boys and 3 girls. How many single matches can be arranged between the two teams when a boy plays against a boy and a girl plays against a girl?
How many A.P.'s with 10 terms are there whose first term is in the set {1, 2, 3} and whose common difference is in the set {1, 2, 3, 4, 5}?
How many three-digit numbers are there?
How many four-digit numbers can be formed with the digits 3, 5, 7, 8, 9 which are greater than 7000, if repetition of digits is not allowed?
Evaluate the following:
From a group of 15 cricket players, a team of 11 players is to be chosen. In how many ways can this be done?
In how many ways can a student choose 5 courses out of 9 courses if 2 courses are compulsory for every student?
In an examination, a student has to answer 4 questions out of 5 questions; questions 1 and 2 are however compulsory. Determine the number of ways in which the student can make the choice.
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has (i) no girl?
Find the number of (ii) triangles
We wish to select 6 persons from 8, but if the person A is chosen, then B must be chosen. In how many ways can the selection be made?
Determine the number of 5 cards combinations out of a deck of 52 cards if there is exactly one ace in each combination.
A parallelogram is cut by two sets of m lines parallel to its sides. Find the number of parallelograms thus formed.
Out of 18 points in a plane, no three are in the same straight line except five points which are collinear. How many (i) straight lines
How many words can be formed by taking 4 letters at a time from the letters of the word 'MORADABAD'?
A business man hosts a dinner to 21 guests. He is having 2 round tables which can accommodate 15 and 6 persons each. In how many ways can he arrange the guests?
Find n if `""^6"P"_2 = "n" ""^6"C"_2`
Find the number of ways of dividing 20 objects in three groups of sizes 8, 7, and 5.
Find the value of 15C4
Find the value of 20C16 – 19C16
We wish to select 6 persons from 8, but if the person A is chosen, then B must be chosen. In how many ways can selections be made?
How many committee of five persons with a chairperson can be selected from 12 persons.
In how many ways can a football team of 11 players be selected from 16 players? How many of them will exclude 2 particular players?
The number of ways in which a team of eleven players can be selected from 22 players always including 2 of them and excluding 4 of them is ______.
The number of ways in which we can choose a committee from four men and six women so that the committee includes at least two men and exactly twice as many women as men is ______.
Three balls are drawn from a bag containing 5 red, 4 white and 3 black balls. The number of ways in which this can be done if at least 2 are red is ______.
In a football championship, 153 matches were played, Every two teams played one match with each other. The number of teams, participating in the championship is ______.
Eighteen guests are to be seated, half on each side of a long table. Four particular guests desire to sit on one particular side and three others on other side of the table. The number of ways in which the seating arrangements can be made is `(11!)/(5!6!) (9!)(9!)`.
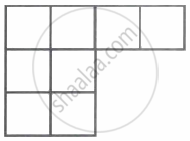
The no. of different ways, the letters of the word KUMARI can be placed in the 8 boxes of the given figure so that no row remains empty will be ______.