Advertisements
Advertisements
Questions
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32.
Using integration, find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32.
Solution 1
y = x ...(1)
x2 + y2 = 32 ...(2)
The region enclosed by y = x and x2 + y2 = 32 is shown in the following figure:
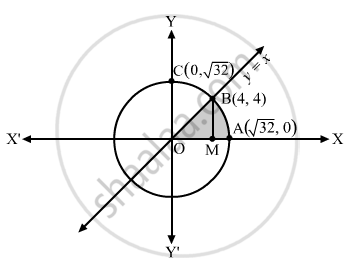
On solving (1) and (2) we find that the given line and circle meet at B(4, 4) in the first quadrant. Let us draw BM perpendicular to the x-axis.
Now, required area = area of triangle BOM + area of region BMAB
Area of triangle BOM `=int_0^4ydx=int_0^4xdx=1/2[x^2/2]_0^4=8.........(3)`
Area of region BMAB= `int_0^sqrt32ydx=int_0^sqrt32sqrt(32-x^2)`
`=[1/2xxsqrt(32-x^2)+1/2xx32xxsin^(-1)(x/sqrt32)]_4^sqrt32`
`=(1/2 xx sqrt32 xx 0+1/2xx 32 xx sin^(−1)(1))−(1/2 xx 4xx 4+1/2 xx 32 xx sin^ (−1)(1/sqrt2))`
`=8π−8−4π`
∴ Area of triangle BOM=4π−8 ... (4)
On adding (3) and (4), we have:
Required area =`8+4π−8=4π`
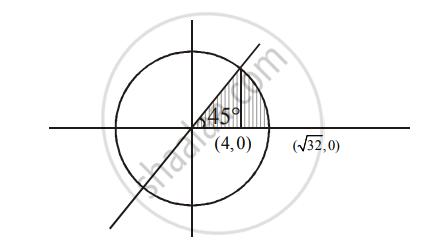
Solution 2
Put y = x in `x^2 + y^2 = 32`
`:. x^2 + x^2 = 32`
`2x^2 = 32`
`x^2 = 16`
x = 4
`A = int_0^4 y_"line" dx + int_4^(sqrt32) y_"circle" dx`
`A = int_0^4 xdx + int_4^(sqrt32) (sqrt(32-x^2))dx`
`= (x^2/2)_0^4 + int_4^(sqrt32) sqrt((sqrt32)^2 - x^2 )dx`
`= (8) + (x/2 sqrt(32-x^2) + 32/2 sin^(-1) (x/sqrt32))^(sqrt32)`
`= (8) + (0 + 16 xx pi/2 - (2sqrt16 + 16sin^(-1) (4/sqrt32)))`
`= 8 + 8pi - 8 - 16 sin^(-1) (1/sqrt2)`
`= 8pi - 16 xx pi/4 = 8pi - 4pi = 4pi sq unit`
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9 = 1.`
Sketch the graph of y = |x + 3| and evaluate `int_(-6)^0 |x + 3|dx`
Find the area enclosed between the parabola y2 = 4ax and the line y = mx
Find the area of the smaller region bounded by the ellipse `x^2/9 + y^2/4` and the line `x/3 + y/2 = 1`
Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and x-axis
Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
Find the equation of an ellipse whose latus rectum is 8 and eccentricity is `1/3`
Find the area of the region bounded by the following curves, the X-axis, and the given lines:
y = `sqrt(6x + 4), x = 0, x = 2`
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y = 5x + 7, x = 2, x = 8
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is _______.
State whether the following is True or False :
The area bounded by the curve y = f(x), X-axis and lines x = a and x = b is `|int_"a"^"b" f(x)*dx|`.
If the curve, under consideration, is below the X-axis, then the area bounded by curve, X-axis and lines x = a, x = b is positive.
State whether the following is True or False :
The area of the portion lying above the X-axis is positive.
Choose the correct alternative:
Area of the region bounded by the curve x2 = 8y, the positive Y-axis lying in the first quadrant and the lines y = 4 and y = 9 is ______
State whether the following statement is True or False:
The area of portion lying below the X axis is negative
The area bounded by the parabola x2 = 9y and the lines y = 4 and y = 9 in the first quadrant is ______
The area of the region bounded by y2 = 25x, x = 1 and x = 2 the X axis is ______
The ratio in which the area bounded by the curves y2 = 8x and x2 = 8y is divided by the line x = 2 is ______
The area of the region bounded by the X-axis and the curves defined by y = cot x, `(pi/6 ≤ x ≤ pi/4)` is ______.
The area enclosed by the parabolas x = y2 - 1 and x = 1 - y2 is ______.
Equation of a common tangent to the circle, x2 + y2 – 6x = 0 and the parabola, y2 = 4x, is:
The slope of a tangent to the curve y = 3x2 – x + 1 at (1, 3) is ______.
The area of the region bounded by the curve y = sin x and the x-axis in [–π, π] is ______.
Area in first quadrant bounded by y = 4x2, x = 0, y = 1 and y = 4 is ______.
Area bounded by the curves y = `"e"^(x^2)`, the x-axis and the lines x = 1, x = 2 is given to be α square units. If the area bounded by the curve y = `sqrt(ℓ "n"x)`, the x-axis and the lines x = e and x = e4 is expressed as (pe4 – qe – α), (where p and q are positive integers), then (p + q) is ______.
The figure shows as triangle AOB and the parabola y = x2. The ratio of the area of the triangle AOB to the area of the region AOB of the parabola y = x2 is equal to ______.
The area bounded by the curve, y = –x, X-axis, x = 1 and x = 4 is ______.
Find the area of the regions bounded by the line y = −2x, the X-axis and the lines x = −1 and x = 2.
