Advertisements
Advertisements
Question
Construct a tangent to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
Solution
Given, a point M’ is at a distance of 6 cm from the centre of a circle of radius 4 cm.
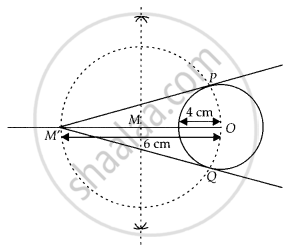
Steps of construction:
- Draw a circle of radius 4 cm. Let centre of this circle is O.
- Join OM’ and bisect it. Let M be mid-point of OM’.
- Taking M as centre and MO as radius draw a circle to intersect circle (0, 4) at two points, P and Q.
- Join PM’ and QM’. PM’ and QM’ are the required tangents from M’ to circle C(0, 4).
APPEARS IN
RELATED QUESTIONS
Draw a line segment AB of length 7 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle.Steps
In the figure given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°,
find the value of x, y and z.

In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
1) AB.
2) the length of tangent PT.

Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60°.
Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Draw a circle of radius 3.5 cm. Take two points A and B on one of its extended diameter, each at a distance of 5 cm from its center. Draw tangents to the circle from each of these points A and B.
Draw a circle of radius 32 cm. Draw a tangent to the circle making an angle 30° with a line passing through the centre.
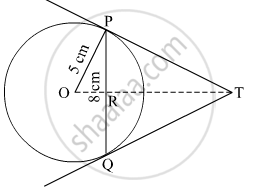
In Figure 2, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
