Advertisements
Advertisements
Question
Evaluate the following definite integrals as limit of sums.
`int_1^4 (x^2 - x) dx`
Solution


From equations (2) and (3), we obtain
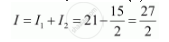
APPEARS IN
RELATED QUESTIONS
Evaluate the following definite integrals as limit of sums.
`int_2^3 x^2 dx`
Evaluate the following definite integrals as limit of sums `int_(-1)^1 e^x dx`
Evaluate the following definite integrals as limit of sums.
`int_0^4 (x + e^(2x)) dx`
Evaluate the definite integral:
`int_(pi/2)^pi e^x ((1-sinx)/(1-cos x)) dx`
Evaluate the definite integral:
`int_0^(pi/4) (sinx cos x)/(cos^4 x + sin^4 x)`dx
Evaluate the definite integral:
`int_0^(pi/4) (sin x + cos x)/(9+16sin 2x) dx`
Evaluate the definite integral:
`int_0^(pi/2) sin 2x tan^(-1) (sinx) dx`
Evaluate the definite integral:
`int_1^4 [|x - 1|+ |x - 2| + |x -3|]dx`
Prove the following:
`int_1^3 dx/(x^2(x +1)) = 2/3 + log 2/3`
Prove the following:
`int_0^(pi/2) sin^3 xdx = 2/3`
Prove the following:
`int_0^(pi/4) 2 tan^3 xdx = 1 - log 2`
`int (cos 2x)/(sin x + cos x)^2dx` is equal to ______.
Evaluate : `int_1^3 (x^2 + 3x + e^x) dx` as the limit of the sum.
Evaluate the following integral:
Evaluate the following integrals as limit of sums:
\[\int\frac{\sqrt{\tan x}}{\sin x \cos x} dx\]
Using L’Hospital Rule, evaluate: `lim_(x->0) (8^x - 4^x)/(4x
)`
Solve: (x2 – yx2) dy + (y2 + xy2) dx = 0
If f and g are continuous functions in [0, 1] satisfying f(x) = f(a – x) and g(x) + g(a – x) = a, then `int_0^"a" "f"(x) * "g"(x)"d"x` is equal to ______.
Evaluate the following:
`int_0^2 ("d"x)/("e"^x + "e"^-x)`
Evaluate the following:
`int_0^pi x sin x cos^2x "d"x`
The value of `lim_(x -> 0) [(d/(dx) int_0^(x^2) sec^2 xdx),(d/(dx) (x sin x))]` is equal to
Left `f(x) = {{:(1",", "if x is rational number"),(0",", "if x is irrational number"):}`. The value `fof (sqrt(3))` is
