Advertisements
Advertisements
Question
Find the mean and variance of the number randomly selected from 1 to 15
Solution
The sample space of the experiment is S = {1, 2, 3,…,15}
Let X denotes the selected number.
Then X is a random variable which can take values 1, 2, 3, …, 15.
∴ P(1) = P(2) = P(3) = … = P(15) = `1/15`
E(X) = `sum_("i" = 1)^"n" x_"i""P"_"i"`
= `1 xx 1/15 + 2 xx 1/15 + 3 xx 1/15 + ... + 15 xx 1/15`
= `(1 + 2 + 3 + ... + 15) xx 1/15`
= `((15 xx 16)/2) xx 1/15`
= 8
Var(X) = `(sum_("i" = 1)^"n"x_"i"^2"p"_"i") - (sum_("i" = 1)^"n"x_"i""p"_"i")^2`
= `1^2 xx 1/15 + 2^2 xx 1/15 + 3^2 xx 1/15 + ... + 15^2 xx 1/15 - (8)^2`
= `(1^2 + 2^2 + 3^2 + ... + 15^2) xx 1/15 - (8)^2`
= `((15 xx 16 xx 31)/6) xx 1/15 - (8)^2`
= 82.67 – 64
= 18.67
APPEARS IN
RELATED QUESTIONS
From a lot of 15 bulbs which include 5 defectives, a sample of 4 bulbs is drawn one by one with replacement. Find the probability distribution of number of defective bulbs. Hence find the mean of the distribution.
An urn contains 5 red and 2 black balls. Two balls are randomly drawn. Let X represents the number of black balls. What are the possible values of X? Is X a random variable?
Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as
(i) number greater than 4
(ii) six appears on at least one die
There are 4 cards numbered 1, 3, 5 and 7, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on the two drawn cards. Find the mean 'and variance of X.
Which of the following distributions of probabilities of a random variable X are the probability distributions?
(i)
| X : | 3 | 2 | 1 | 0 | −1 |
| P (X) : | 0.3 | 0.2 | 0.4 | 0.1 | 0.05 |
| X : | 0 | 1 | 2 |
| P (X) : | 0.6 | 0.4 | 0.2 |
(iii)
| X : | 0 | 1 | 2 | 3 | 4 |
| P (X) : | 0.1 | 0.5 | 0.2 | 0.1 | 0.1 |
(iv)
| X : | 0 | 1 | 2 | 3 |
| P (X) : | 0.3 | 0.2 | 0.4 | 0.1 |
A random variable X has the following probability distribution:
| Values of X : | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P (X) : | a | 3a | 5a | 7a | 9a | 11a | 13a | 15a | 17a |
Determine:
(i) The value of a
(ii) P (X < 3), P (X ≥ 3), P (0 < X < 5).
The probability distribution function of a random variable X is given by
| xi : | 0 | 1 | 2 |
| pi : | 3c3 | 4c − 10c2 | 5c-1 |
where c > 0 Find: c
The probability distribution function of a random variable X is given by
| xi : | 0 | 1 | 2 |
| pi : | 3c3 | 4c − 10c2 | 5c-1 |
where c > 0 Find: P (X < 2)
A random variable X takes the values 0, 1, 2 and 3 such that:
P (X = 0) = P (X > 0) = P (X < 0); P (X = −3) = P (X = −2) = P (X = −1); P (X = 1) = P (X = 2) = P (X = 3) . Obtain the probability distribution of X.
Two cards are drawn from a well shuffled pack of 52 cards. Find the probability distribution of the number of aces.
Four cards are drawn simultaneously from a well shuffled pack of 52 playing cards. Find the probability distribution of the number of aces.
Two cards are drawn successively with replacement from well shuffled pack of 52 cards. Find the probability distribution of the number of aces.
Two cards are drawn successively with replacement from a well shuffled pack of 52 cards. Find the probability distribution of the number of kings.
From a lot containing 25 items, 5 of which are defective, 4 are chosen at random. Let X be the number of defectives found. Obtain the probability distribution of X if the items are chosen without replacement .
An urn contains 4 red and 3 blue balls. Find the probability distribution of the number of blue balls in a random draw of 3 balls with replacement.
From a lot of 10 bulbs, which includes 3 defectives, a sample of 2 bulbs is drawn at random. Find the probability distribution of the number of defective bulbs.
Find the mean and standard deviation of each of the following probability distributions:
| xi : | 2 | 3 | 4 |
| pi : | 0.2 | 0.5 | 0.3 |
Find the mean and standard deviation of each of the following probability distribution :
| xi : | -5 | -4 | 1 | 2 |
| pi : | \[\frac{1}{4}\] | \[\frac{1}{8}\] | \[\frac{1}{2}\] | \[\frac{1}{8}\] |
Find the mean and standard deviation of each of the following probability distribution :
| xi: | 0 | 1 | 3 | 5 |
| pi : | 0.2 | 0.5 | 0.2 | 0.1 |
A discrete random variable X has the probability distribution given below:
| X: | 0.5 | 1 | 1.5 | 2 |
| P(X): | k | k2 | 2k2 | k |
Find the value of k.
A discrete random variable X has the probability distribution given below:
| X: | 0.5 | 1 | 1.5 | 2 |
| P(X): | k | k2 | 2k2 | k |
Determine the mean of the distribution.
Find the mean variance and standard deviation of the following probability distribution
| xi : | a | b |
| pi : | p | q |
Two cards are drawn simultaneously from a pack of 52 cards. Compute the mean and standard deviation of the number of kings.
A fair die is tossed. Let X denote twice the number appearing. Find the probability distribution, mean and variance of X.
A die is tossed twice. A 'success' is getting an odd number on a toss. Find the variance of the number of successes.
Write the values of 'a' for which the following distribution of probabilities becomes a probability distribution:
| X= xi: | -2 | -1 | 0 | 1 |
| P(X= xi) : |
\[\frac{1 - a}{4}\]
|
\[\frac{1 + 2a}{4}\]
|
\[\frac{1 - 2a}{4}\]
|
\[\frac{1 + a}{4}\]
|
Find the mean of the following probability distribution:
| X= xi: | 1 | 2 | 3 |
| P(X= xi) : |
\[\frac{1}{4}\]
|
\[\frac{1}{8}\]
|
\[\frac{5}{8}\]
|
If a random variable X has the following probability distribution:
| X : | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P (X) : | a | 3a | 5a | 7a | 9a | 11a | 13a | 15a | 17a |
then the value of a is
A random variable X takes the values 0, 1, 2, 3 and its mean is 1.3. If P (X = 3) = 2 P (X = 1) and P (X = 2) = 0.3, then P (X = 0) is
Mark the correct alternative in the following question:
The probability distribution of a discrete random variable X is given below:
| X: | 2 | 3 | 4 | 5 |
| P(X): |
\[\frac{5}{k}\]
|
\[\frac{7}{k}\]
|
\[\frac{9}{k}\]
|
\[\frac{11}{k}\] |
The value of k is .
Find the probability distribution of the number of doublets in three throws of a pair of dice and find its mean.
Three cards are drawn successively with replacement from a well shuffled pack of 52 cards. Find the probability distribution of the number of spades. Hence, find the mean of the distribtution.
Five bad oranges are accidently mixed with 20 good ones. If four oranges are drawn one by one successively with replacement, then find the probability distribution of number of bad oranges drawn. Hence find the mean and variance of the distribution.
Using the truth table verify that p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r).
Find mean and standard deviation of the continuous random variable X whose p.d.f. is given by f(x) = 6x(1 - x);= (0); 0 < x < 1(otherwise)
John and Mathew started a business with their capitals in the ratio 8 : 5. After 8 months, john added 25% of his earlier capital as further investment. At the same time, Mathew withdrew 20% of bis earlier capital. At the end of the year, they earned ₹ 52000 as profit. How should they divide the profit between them?
A departmental store gives trafnfng to the salesmen in service followed by a test. It is experienced that the performance regarding sales of any salesman is linearly related to the scores secured by him. The following data gives the test scores and sales made by nine (9) salesmen during a fixed period.
| Test scores (X) | 16 | 22 | 28 | 24 | 29 | 25 | 16 | 23 | 24 |
| Sales (Y) (₹ in hundreds) | 35 | 42 | 57 | 40 | 54 | 51 | 34 | 47 | 45 |
(a) Obtain the line of regression of Y on X.
(b) Estimate Y when X = 17.
If random variable X has probability distribution function.
f(x) = `c/x`, 1 < x < 3, c > 0, find c, E(x) and Var(X)
The expenditure Ec of a person with income I is given by Ec = (0.000035) I2 + (0. 045) I. Find marginal propensity to consume (MPC) and average propensity to consume (APC) when I = 5000.
If X ∼ N (4,25), then find P(x ≤ 4)
The following table gives the age of the husbands and of the wives :
| Age of wives (in years) |
Age of husbands (in years) |
|||
| 20-30 | 30- 40 | 40- 50 | 50- 60 | |
| 15-25 | 5 | 9 | 3 | - |
| 25-35 | - | 10 | 25 | 2 |
| 35-45 | - | 1 | 12 | 2 |
| 45-55 | - | - | 4 | 16 |
| 55-65 | - | - | - | 4 |
Find the marginal frequency distribution of the age of husbands.
Solve the following:
Identify the random variable as either discrete or continuous in each of the following. Write down the range of it.
A highway safety group is interested in studying the speed (km/hrs) of a car at a check point.
The p.d.f. of r.v. of X is given by
f (x) = `k /sqrtx` , for 0 < x < 4 and = 0, otherwise. Determine k .
Determine c.d.f. of X and hence P (X ≤ 2) and P(X ≤ 1).
A pair of dice is thrown 3 times. If getting a doublet is considered a success, find the probability of two successes
The probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5) that fuse after 200 days of use. Find the probability of X = 0
The probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5) that fuse after 200 days of use. Find the probability of X > 1
The probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5) that fuse after 200 days of use. Find the probability of (i) X = 0, (ii) X ≤ 1, (iii) X > 1, (iv) X ≥ 1.
Solve the following problem :
Find the probability of the number of successes in two tosses of a die, where success is defined as number greater than 4.
Solve the following problem :
Find the probability of the number of successes in two tosses of a die, where success is defined as six appears in at least one toss.
Solve the following problem :
The probability that a bomb will hit the target is 0.8. Find the probability that, out of 5 bombs, exactly 2 will miss the target.
Solve the following problem :
The probability that a component will survive a check test is 0.6. Find the probability that exactly 2 of the next 4 components tested survive.
Solve the following problem :
It is observed that it rains on 10 days out of 30 days. Find the probability that it rains on exactly 3 days of a week.
Let the p.m.f. of a random variable X be P(x) = `(3 - x)/10`, for x = −1, 0, 1, 2 = 0, otherwise Then E(x) is ______
For the random variable X, if V(X) = 4, E(X) = 3, then E(x2) is ______
Find the probability distribution of the number of doublets in three throws of a pair of dice
Four balls are to be drawn without replacement from a box containing 8 red and 4 white balls. If X denotes the number of red ball drawn, find the probability distribution of X.
A discrete random variable X has the probability distribution given as below:
| X | 0.5 | 1 | 1.5 | 2 |
| P(X) | k | k2 | 2k2 | k |
Find the value of k
A discrete random variable X has the probability distribution given as below:
| X | 0.5 | 1 | 1.5 | 2 |
| P(X) | k | k2 | 2k2 | k |
Determine the mean of the distribution.
The probability distribution of a random variable X is given below:
| X | 0 | 1 | 2 | 3 |
| P(X) | k | `"k"/2` | `"k"/4` | `"k"/8` |
Determine the value of k.
Two biased dice are thrown together. For the first die P(6) = `1/2`, the other scores being equally likely while for the second die, P(1) = `2/5` and the other scores are equally likely. Find the probability distribution of ‘the number of ones seen’.
Find the probability distribution of the maximum of the two scores obtained when a die is thrown twice. Determine also the mean of the distribution.
The random variable X can take only the values 0, 1, 2. Given that P(X = 0) = P(X = 1) = p and that E(X2) = E[X], find the value of p
The probability distribution of a random variable x is given as under:
P(X = x) = `{{:("k"x^2, "for" x = 1"," 2"," 3),(2"k"x, "for" x = 4"," 5"," 6),(0, "otherwise"):}`
where k is a constant. Calculate E(3X2)
The probability distribution of a discrete random variable X is given below:
| X | 2 | 3 | 4 | 5 |
| P(X) | `5/"k"` | `7/"k"` | `9/"k"` | `11/"k"` |
The value of k is ______.
A random variable x has to following probability distribution.
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(x) | 0 | k | 2k | 2k | 3k | k2 | 2k2 | 7k2 + k |
Determine
A person throws two fair dice. He wins ₹ 15 for throwing a doublet (same numbers on the two dice), wins ₹ 12 when the throw results in the sum of 9, and loses ₹ 6 for any other outcome on the throw. Then the expected gain/loss (in ₹) of the person is ______.
Two balls are drawn at random one by one with replacement from an urn containing equal number of red balls and green balls. Find the probability distribution of number of red balls. Also, find the mean of the random variable.
Two numbers are selected from first six even natural numbers at random without replacement. If X denotes the greater of two numbers selected, find the probability distribution of X.
A box contains 30 fruits, out of which 10 are rotten. Two fruits are selected at random one by one without replacement from the box. Find the probability distribution of the number of unspoiled fruits. Also find the mean of the probability distribution.
Kiran plays a game of throwing a fair die 3 times but to quit as and when she gets a six. Kiran gets +1 point for a six and –1 for any other number.
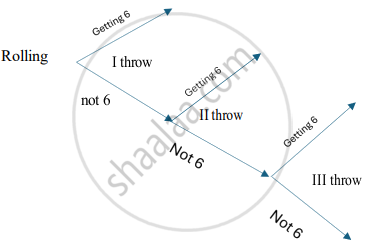
- If X denotes the random variable “points earned” then what are the possible values X can take?
- Find the probability distribution of this random variable X.
- Find the expected value of the points she gets.
