Advertisements
Advertisements
Question
If `2^x xx3^yxx5^z=2160,` find x, y and z. Hence, compute the value of `3^x xx2^-yxx5^-z.`
Solution
Given `2^x xx3^yxx5^z=2160`
First, find out the prime factorisation of 2160.
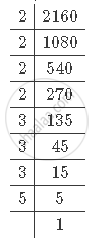
It can be observed that 2160 can be written as `2^4xx3^3xx5^1`
Also,
`2^x xx36yxx5^z=2^4xx3^3xx5^1`
⇒ x = 4, y = 3, z = 1
Therefore, the value of `3^x xx2^-yxx5^-z` is `3^4xx2^-3xx5^-1=81xx1/8xx1/5=81/40`
APPEARS IN
RELATED QUESTIONS
Simplify:-
`2^(2/3). 2^(1/5)`
Prove that:
`(x^a/x^b)^cxx(x^b/x^c)^axx(x^c/x^a)^b=1`
Solve the following equation for x:
`2^(x+1)=4^(x-3)`
Prove that:
`(2^n+2^(n-1))/(2^(n+1)-2^n)=3/2`
If a and b are different positive primes such that
`((a^-1b^2)/(a^2b^-4))^7div((a^3b^-5)/(a^-2b^3))=a^xb^y,` find x and y.
If a and b are different positive primes such that
`(a+b)^-1(a^-1+b^-1)=a^xb^y,` find x + y + 2.
If `a=x^(m+n)y^l, b=x^(n+l)y^m` and `c=x^(l+m)y^n,` Prove that `a^(m-n)b^(n-l)c^(l-m)=1`
State the product law of exponents.
If \[\frac{3^{2x - 8}}{225} = \frac{5^3}{5^x},\] then x =
The simplest rationalising factor of \[\sqrt{3} + \sqrt{5}\] is ______.
