Advertisements
Advertisements
Question
If 1176 = `2^axx3^bxx7^c,` find the values of a, b and c. Hence, compute the value of `2^axx3^bxx7^-c` as a fraction.
Solution
First find the prime factorisation of 1176.
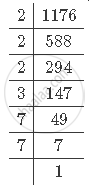
It can be observed that 1176 can be written as `2^3xx3^1xx7^2`
`1176=2^a3^b7^c=2^3 3^1 7^2`
So, a = 3, b = 1 and c = 2.
Therefore, the value of `2^a xx3^bxx76-c` is `2^3xx3^1xx7^-2=8xx3xx1/49=24/49`
APPEARS IN
RELATED QUESTIONS
Assuming that x, y, z are positive real numbers, simplify the following:
`(sqrtx)^((-2)/3)sqrt(y^4)divsqrt(xy^((-1)/2))`
Simplify:
`(16^(-1/5))^(5/2)`
Simplify:
`(sqrt2/5)^8div(sqrt2/5)^13`
If ax = by = cz and b2 = ac, show that `y=(2zx)/(z+x)`
Find the value of x in the following:
`5^(2x+3)=1`
If a and b are different positive primes such that
`((a^-1b^2)/(a^2b^-4))^7div((a^3b^-5)/(a^-2b^3))=a^xb^y,` find x and y.
If 24 × 42 =16x, then find the value of x.
For any positive real number x, find the value of \[\left( \frac{x^a}{x^b} \right)^{a + b} \times \left( \frac{x^b}{x^c} \right)^{b + c} \times \left( \frac{x^c}{x^a} \right)^{c + a}\].
`(2/3)^x (3/2)^(2x)=81/16 `then x =
If \[x = \sqrt{6} + \sqrt{5}\],then \[x^2 + \frac{1}{x^2} - 2 =\]
