Advertisements
Advertisements
प्रश्न
If 1176 = `2^axx3^bxx7^c,` find the values of a, b and c. Hence, compute the value of `2^axx3^bxx7^-c` as a fraction.
उत्तर
First find the prime factorisation of 1176.
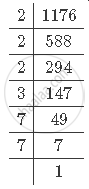
It can be observed that 1176 can be written as `2^3xx3^1xx7^2`
`1176=2^a3^b7^c=2^3 3^1 7^2`
So, a = 3, b = 1 and c = 2.
Therefore, the value of `2^a xx3^bxx76-c` is `2^3xx3^1xx7^-2=8xx3xx1/49=24/49`
APPEARS IN
संबंधित प्रश्न
Find:-
`64^(1/2)`
Find:-
`9^(3/2)`
If a = 3 and b = -2, find the values of :
aa + bb
Prove that:
`(x^a/x^b)^(a^2+ab+b^2)xx(x^b/x^c)^(b^2+bc+c^2)xx(x^c/x^a)^(c^2+ca+a^2)=1`
Prove that:
`(a^-1+b^-1)^-1=(ab)/(a+b)`
Solve the following equations for x:
`2^(2x)-2^(x+3)+2^4=0`
Assuming that x, y, z are positive real numbers, simplify the following:
`(x^((-2)/3)y^((-1)/2))^2`
Show that:
`((a+1/b)^mxx(a-1/b)^n)/((b+1/a)^mxx(b-1/a)^n)=(a/b)^(m+n)`
Write \[\left( 625 \right)^{- 1/4}\] in decimal form.
If \[x = \sqrt{6} + \sqrt{5}\],then \[x^2 + \frac{1}{x^2} - 2 =\]
