Advertisements
Advertisements
प्रश्न
If `2^x xx3^yxx5^z=2160,` find x, y and z. Hence, compute the value of `3^x xx2^-yxx5^-z.`
उत्तर
Given `2^x xx3^yxx5^z=2160`
First, find out the prime factorisation of 2160.
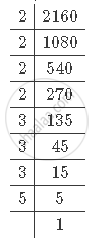
It can be observed that 2160 can be written as `2^4xx3^3xx5^1`
Also,
`2^x xx36yxx5^z=2^4xx3^3xx5^1`
⇒ x = 4, y = 3, z = 1
Therefore, the value of `3^x xx2^-yxx5^-z` is `3^4xx2^-3xx5^-1=81xx1/8xx1/5=81/40`
APPEARS IN
संबंधित प्रश्न
If a = 3 and b = -2, find the values of :
ab + ba
Assuming that x, y, z are positive real numbers, simplify the following:
`sqrt(x^3y^-2)`
Prove that:
`sqrt(3xx5^-3)divroot3(3^-1)sqrt5xxroot6(3xx5^6)=3/5`
Prove that:
`(1/4)^-2-3xx8^(2/3)xx4^0+(9/16)^(-1/2)=16/3`
Prove that:
`(3^-3xx6^2xxsqrt98)/(5^2xxroot3(1/25)xx(15)^(-4/3)xx3^(1/3))=28sqrt2`
Show that:
`(x^(1/(a-b)))^(1/(a-c))(x^(1/(b-c)))^(1/(b-a))(x^(1/(c-a)))^(1/(c-b))=1`
If 2x = 3y = 6-z, show that `1/x+1/y+1/z=0`
Write the value of \[\left\{ 5( 8^{1/3} + {27}^{1/3} )^3 \right\}^{1/4} . \]
The square root of 64 divided by the cube root of 64 is
If a, b, c are positive real numbers, then \[\sqrt[5]{3125 a^{10} b^5 c^{10}}\] is equal to
