Advertisements
Advertisements
Question
If A, B, C, D are angles of a cyclic quadrilateral, prove that: cos A + cos B + cos C + cos D = 0.
Solution
In a cyclic quadrilateral sum of opposite angles are 180°.
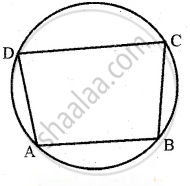
Since A, B, C, D are angles of cyclic quadrilateral
A + C = 180° and B + D = 180°
LHS = cos A + cos B + cos C + cos D
= cos A + cos B + cos(180° – A) + cos(180° – B)
= cos A + cos B – cos A – cos B
= 0
= RHS
APPEARS IN
RELATED QUESTIONS
Convert the following degree measure into radian measure.
60°
Find the degree measure corresponding to the following radian measure.
`(9pi)/5`
Find the degree measure corresponding to the following radian measure.
`(11pi)/18`
Find the values of the following trigonometric ratio.
tan(-855°)
Find the values of the following trigonometric ratio.
cosec 1125°
Prove that:
2 sin2 `pi/6` + cosec2 `(7pi)/6` cos2 `pi/3 = 3/2`
Prove that:
tan(π + x) cot(x – π) – cos(2π – x) cos(2π + x) = sin2 x.
Prove that:
`(sin(180^circ + "A")cos(90^circ - "A")tan(270^circ - "A"))/(sec(540^circ - "A") cos(360^circ + "A") "cosec"(270^circ + "A"))` = - sin A cos2 A.
Prove that:
`(cos 4x + cos 3x + cos 2x)/(sin 4x + sin 3x + sin 2x)` = cot 3x
`((cos x)/(cosec x)) - sqrt(1 - sin^2x) sqrt(1 - cos^2 x)` is:
