Advertisements
Advertisements
Question
If sin A = `(sqrt3)/(2)` and cos B = `(sqrt3)/(2)` , find the value of : `(tan"A" – tan"B")/(1+tan"A" tan"B")`
Solution
Consider the diagram below :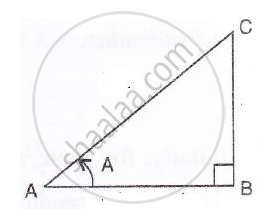 'in A = `(sqrt3)/(2)`
'in A = `(sqrt3)/(2)`
i.e.`"perpendicular"/"hypotenuse" = (sqrt3)/(2) ⇒"BC"/"AC" = (sqrt3)/(2)`
Therefore if length of BC = `sqrt3x`, length of AC = 2x
Since
AB2 + BC2 = AC2 ...[ Using Pythagoras Therorm]
`(sqrt3x)^2 + AB^2 = (2x)^2`
AB2 = x2
∴ AB = x (base)
Consider the diagram below :
cos B = `(sqrt3)/(2)`
i.e.`"base"/"perpendicular" = (sqrt3)/(2) ⇒ "AB"/"BC" = (sqrt3)/(2)`
Therefore if length of AB = `sqrt3x` , length of BC = 2x
Since
AB2 + AC2 = BC2 ...[ Using Pythagoras Theorem ]
AC2 + `(sqrt3x)^2 = (2x)^2`
AC2 = x2
∴ AC = x(perpendicular)
Now
tan A = `"perpendicular"/"base" = (sqrt3x)/(x) = sqrt3`
tan B = `"perpendicular"/"base" = (x)/(sqrt3x) = 1/(sqrt3)`
Therefore
`(tan A – tan B)/(1 + tan A tan B) = (sqrt3 - 1/(sqrt3))/(1+sqrt3 1/(sqrt3)`
= `((2)/(sqrt3))/(2)`
= `(1)/(sqrt3)`
APPEARS IN
RELATED QUESTIONS
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
If A and B are acute angles such that tan A = 1/2, tan B = 1/3 and tan (A + B) = `(tan A + tan B)/(1- tan A tan B)` A + B = ?
If x = cot A + cos A and y = cot A – cos A then prove that `((x-y)/(x+y))^2 + ((x-y)/2)^2=1`
In the adjoining figure, ΔABC is right-angled at B and ∠A = 450. If AC = 3`sqrt(2)`cm, find (i) BC, (ii) AB.
If 3x = cosecθ = and `3/x= cottheta` find the value of 3`(x^2-1/x^2)`.
If sin (A+B) = sin A cos B + cos A sin B and cos (A-B) = cos A cos B + sin A sin B
(i) sin (750)
(ii) cos (150)
`(cos 28°)/(sin 62°)` = ?
Given q tan A = p, find the value of:
`("p" sin "A" – "q" cos "A")/("p" sin "A" + "q" cos "A")`.
If cosec A + sin A = 5`(1)/(5)`, find the value of cosec2A + sin2A.
Evaluate: `5/(cot^2 30^circ) + 1/(sin^2 60^circ) - cot^2 45^circ + 2 sin^2 90^circ`.
