Advertisements
Advertisements
Question
In a school, 100 pupils have heights as tabulate below:
| Height (in cm) | No. of pupils |
| 121 – 130 | 12 |
| 131 – 140 | 16 |
| 141 – 150 | 30 |
| 151 – 160 | 20 |
| 161 – 170 | 14 |
| 171 – 180 | 8 |
Find the median height by drawing an ogive.
Solution
| Exclusive class Intervals |
Height (in cm) |
No. of pupils |
Cumulative Frequency |
| 120.5 – 130.5 | 121 – 130 | 12 | 12 |
| 130.5 – 140.5 | 131 – 140 | 16 | 28 |
| 140.5 – 150.5 | 141 – 150 | 30 | 58 |
| 150.5 – 160.5 | 151 – 160 | 20 | 78 |
| 160.5 – 170.5 | 161 – 170 | 14 | 92 |
| 170.5 – 180.5 | 171 – 180 | 8 | 100 |
No. of terms = 100 = N
∴ Median = `100/2` = 50th term
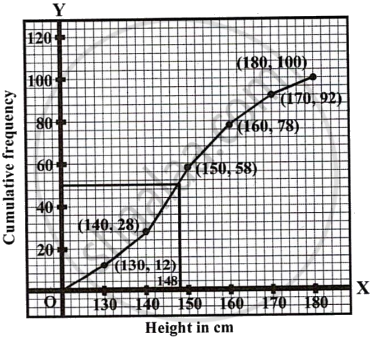
Plotting the points (120.5, 0), (130.5, 12), (140.5, 28), (150.5, 58), (160.5, 78), (170.5, 92), (180.5, 100) on graph paper and join them by free hand curve gives the required ogive.
Through mark 50, draw a line parallel to x-axis which meets the curve at A. From A, draw perpendicular to x-axis which meets x-axis at B is the median which is 148 cm.
APPEARS IN
RELATED QUESTIONS
The marks of 10 students of a class in an examination arranged in ascending order is as follows:
13, 35, 43, 46, x, x + 4, 55, 61, 71, 80
If the median marks is 48, find the value of x. Hence, find the mode of the given data.
Draw a histogram from the following frequency distribution and find the mode from the graph:
| Class | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
| Frequency | 2 | 5 | 18 | 14 | 8 | 5 |
Using the information given in the adjoining histogram, calculate the mean.
Find the median and mode for the set of numbers:
2, 2, 3, 5, 5, 5, 6, 8 and 9
Find the mode of the following frequency distribution:
| Hrs. Spent daily in studies | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 |
| No. of students | 8 | 7 | 3 | 5 | 10 | 6 | 3 | 4 |
Find the median of the following frequency distribution :
| Salarv fin Rs) | 3500 | 4000 | 4500 | 5000 | 5500 | 6000 |
| No. of people | 9 | 17 | 23 | 15 | 6 | 5 |
Find the median of 9, 3, 20, 13, 0, 7 and 10
Find the mean of: first eight natural numbers
Find the mean and the median of: 0.5, 5.6, 3.8, 4.9, 2.7 and 4.4
Find the mean and the median of: 1.2, 1.9, 2.2, 2.6 and 2.9
