Advertisements
Advertisements
Question
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Solution
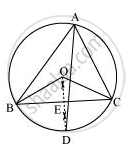
Let perpendicular bisector of side BC and angle bisector of ∠A meet at point D. Let the perpendicular bisector of side BC intersect it at E.
Perpendicular bisector of side BC will pass through circumcentre O of the circle. ∠BOC and ∠BAC are the angles subtended by arc BC at the centre and a point A on the remaining part of the circle respectively. We also know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
∠BOC = 2 ∠BAC = 2 ∠A ... (1)
In ΔBOE and ΔCOE,
OE = OE (Common)
OB = OC (Radii of same circle)
∠OEB = ∠OEC (Each 90° as OD ⊥ BC)
∴ ΔBOE ≅ ∠COE (RHS congruence rule)
∠BOE = ∠COE (By CPCT) ... (2)
However, ∠BOE + ∠COE = ∠BOC
⇒ ∠BOE +∠BOE = 2 ∠A [Using equations (1) and (2)]
⇒ 2 ∠BOE = 2 ∠A
⇒ ∠BOE = ∠A
∴ ∠BOE = ∠COE = ∠A
The perpendicular bisector of side BC and angle bisector of ∠A meet at point D.
∴ ∠BOD = ∠BOE = ∠A ... (3)
Since AD is the bisector of angle ∠A,
∠BAD = ∠A/2
⇒ 2 ∠BAD = ∠A ... (4)
From equations (3) and (4), we obtain
∠BOD = 2 ∠BAD
This can be possible only when point BD will be a chord of the circle. For this, the point D lies on the circum circle.
Therefore, the perpendicular bisector of side BC and the angle bisector of ∠A meet on the circum circle of triangle ABC.
APPEARS IN
RELATED QUESTIONS
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Prove that a cyclic parallelogram is a rectangle.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
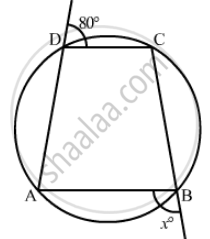
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
