Advertisements
Advertisements
Question
In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(ar(ABC))/(ar(DBC)) = (AO)/(DO)`
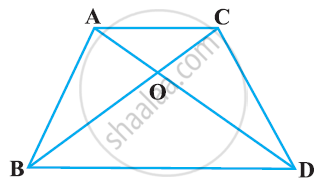
Solution
Let us draw two perpendiculars AP and DM on line BC.
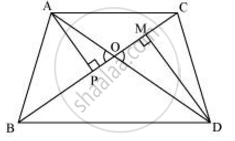
We know that area of a triangle = `1/2 xx "Base" xx "Height"`
`:.(ar(triangleABC))/(ar(triangleDBC)) = (1/2 BC xx AP)/(1/2BC xx DM) = (AP)/(DM)`
In ΔAPO and ΔDMO,
∠APO = ∠DMO (Each = 90°)
∠AOP = ∠DOM (Vertically opposite angles)
∴ ΔAPO ∼ ΔDMO (By AA similarity criterion)
`:. (AP)/(DM) = (AO)/(DO)`
`=> (ar(triangleABC))/(ar(triangleDBC))=(AO)/(DO)`
APPEARS IN
RELATED QUESTIONS
In two similar triangles ABC and PQR, if their corresponding altitudes AD and PS are in the ratio 4 : 9, find the ratio of the areas of ∆ABC and ∆PQR
D and E are points on the sides AB and AC respectively of a ∆ABC such that DE || BC and divides ∆ABC into two parts, equal in area. Find
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
If the areas of two similar triangles are equal, prove that they are congruent.
Triangles ABC and DEF are similar If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ΔABC and ΔDEF.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
If ∆ABC ~ ∆PQR, A (∆ABC) = 80, A (∆PQR) = 125, then fill in the blanks. \[\frac{A\left( ∆ ABC \right)}{A\left( ∆ . . . . \right)} = \frac{80}{125} \therefore \frac{AB}{PQ} = \frac{......}{......}\]
∆LMN ~ ∆PQR, 9 × A (∆PQR ) = 16 × A (∆LMN). If QR = 20 then Find MN.
If ΔABC ∼ ΔPQR and `(A(ΔABC))/(A(ΔPQR)) = 16/25`, then find AB : PQ.
