Advertisements
Advertisements
Question
In Given Figure, find tan P – cot R.

Solution
Applying Pythagoras theorem for ΔPQR, we obtain
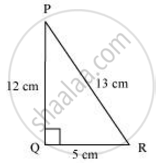
PR2 = PQ2 + QR2
(13 cm)2 = (12 cm)2 + QR2
169 cm2 = 144 cm2 + QR2
25 cm2 = QR2
QR = 5 cm
tan P = `("Side opposite to ∠P")/("Side adjacent to ∠P") = ("QR")/("PQ")`
= `5/12`
cot R = `("Side opposite to ∠R")/("Side adjacent to ∠R") = ("QR")/("PQ")`
= `5/12`
tan P - cot R = `5/12 - 5/12 = 0`
APPEARS IN
RELATED QUESTIONS
State whether the following are true or false. Justify your answer.
cos A is the abbreviation used for the cosecant of angle A.
If `tan theta = a/b`, find the value of `(cos theta + sin theta)/(cos theta - sin theta)`
Evaluate the following
cos2 30° + cos2 45° + cos2 60° + cos2 90°
Evaluate the following
tan2 30° + tan2 60° + tan2 45°
Evaluate the following:
(cosec2 45° sec2 30°)(sin2 30° + 4 cot2 45° − sec2 60°)
Evaluate the Following
`cot^2 30^@ - 2 cos^2 60^circ- 3/4 sec^2 45^@ - 4 sec^2 30^@`
Evaluate the Following
`4/(cot^2 30^@) + 1/(sin^2 60^@) - cos^2 45^@`
Find the value of x in the following :
`2 sin x/2 = 1`
If sin (A − B) = sin A cos B − cos A sin B and cos (A − B) = cos A cos B + sin A sin B, find the values of sin 15° and cos 15°.
If sin 2A = `1/2` tan² 45° where A is an acute angle, then the value of A is ______.
`(sin theta)/(1 + cos theta)` is ______.
If x sin (90° – θ) cot (90° – θ) = cos (90° – θ), then x is equal to ______.
Given that sinα = `1/2` and cosβ = `1/2`, then the value of (α + β) is ______.
If 4 tanθ = 3, then `((4 sintheta - costheta)/(4sintheta + costheta))` is equal to ______.
Let f(x) = sinx.cos3x and g(x) = cosx.sin3x, then the value of `7((f(π/7) + g(π/7))/(g((5π)/14) + f((5π)/14)))` is ______.
If f(x) = `3cos(x + (5π)/6) - 5sinx + 2`, then maximum value of f(x) is ______.
The maximum value of the expression 5cosα + 12sinα – 8 is equal to ______.
If `θ∈[(5π)/2, 3π]` and 2cosθ + sinθ = 1, then the value of 7cosθ + 6sinθ is ______.
If sin θ – cos θ = 0, then find the value of sin4 θ + cos4 θ.
