Advertisements
Advertisements
Question
Is the function defined by `f(x) = {(x+5, if x <= 1),(x -5, if x > 1):}` a continuous function?
Solution
`f (x) = {(x+5, if x<=1),(x - 5, if x > 1):}`
`lim_(x -> 1^-) f(x) = lim_(x -> 1^-)` (x + 5)
= `lim_(h -> 0)` [1 - h + 5]
= `lim_(h -> 0)` (6 - h)
= 6 - 0
= 6
`lim_(x -> 1^+) f(x) = lim_(x -> 1^+)` (x - 5)
= `lim_(h -> 0)` (1 + h - 5)
= `lim_(h -> 0)` (h - 4)
= 0 - 4
= - 4
Hence, f is not continuous at x = 1.
APPEARS IN
RELATED QUESTIONS
Discuss the continuity of the following functions. If the function have a removable discontinuity, redefine the function so as to remove the discontinuity
`f(x)=(4^x-e^x)/(6^x-1)` for x ≠ 0
`=log(2/3) ` for x=0
Find the values of p and q for which
f(x) = `{((1-sin^3x)/(3cos^2x),`
is continuous at x = π/2.
Is the function f defined by f(x)= `{(x, if x<=1),(5, if x > 1):}` continuous at x = 0? At x = 1? At x = 2?
Find all point of discontinuity of f, where f is defined by `f (x) = {(2x + 3, if x<=2),(2x - 3, if x > 2):}`
Find all points of discontinuity of f, where f is defined by `f(x) = {(|x|+3, if x<= -3),(-2x, if -3 < x < 3),(6x + 2, if x >= 3):}`
Find all points of discontinuity of f, where f is defined by `f(x) = {(|x|/x , if x != 0),(0, if x = 0):}`
Find all points of discontinuity of f, where f is defined by `f (x) = {(x+1, if x>=1),(x^2+1, if x < 1):}`
Find all points of discontinuity of f, where f is defined by `f(x) = {(x^3 - 3, if x <= 2),(x^2 + 1, if x > 2):}`
Find the points of discontinuity of f, where `f (x) = {(sinx/x, if x<0),(x + 1, if x >= 0):}`
Determine if f defined by `f(x) = {(x^2 sin 1/x, "," if x != 0),(0, "," if x = 0):}` is a continuous function?
Determine the value of the constant 'k' so that function f(x) `{((kx)/|x|, ","if x < 0),(3"," , if x >= 0):}` is continuous at x = 0
Show that the function f(x) = `{(x^2, x<=1),(1/2, x>1):}` is continuous at x = 1 but not differentiable.
Test the continuity of the function on f(x) at the origin:
\[f\left( x \right) = \begin{cases}\frac{x}{\left| x \right|}, & x \neq 0 \\ 1 , & x = 0\end{cases}\]
In the following, determine the value of constant involved in the definition so that the given function is continuou:
Discuss the Continuity of the F(X) at the Indicated Points : F(X) = | X − 1 | + | X + 1 | at X = −1, 1.
Find the point of discontinuity, if any, of the following function: \[f\left( x \right) = \begin{cases}\sin x - \cos x , & \text{ if } x \neq 0 \\ - 1 , & \text{ if } x = 0\end{cases}\]
Show that the function f given by:
`f(x)={((e^(1/x)-1)/(e^(1/x)+1),"if",x,!=,0),(-1,"if",x,=,0):}"`
is discontinuous at x = 0.
`lim_("x" -> pi/2)` [sinx] is equal to ____________.
The number of discontinuous functions y(x) on [-2, 2] satisfying x2 + y2 = 4 is ____________.
Let f (x) `= (1 - "tan x")/(4"x" - pi), "x" ne pi/4, "x" in (0, pi/2).` If f(x) is continuous in `(0, pi/2), "then f"(pi/4) =` ____________.
If f(x) `= sqrt(4 + "x" - 2)/"x", "x" ne 0` be continuous at x = 0, then f(0) = ____________.
`lim_("x"-> 0) sqrt(1/2 (1 - "cos" 2"x"))/"x"` is equal to
The function `f(x) = (x^2 - 25)/(x + 5)` is continuous at x =
The function f defined by `f(x) = {{:(x, "if" x ≤ 1),(5, "if" x > 1):}` discontinuous at x equal to
Sin |x| is a continuous function for
Let a, b ∈ R, b ≠ 0. Define a function
F(x) = `{{:(asin π/2(x - 1)",", "for" x ≤ 0),((tan2x - sin2x)/(bx^3)",", "for" x > 0):}`
If f is continuous at x = 0, then 10 – ab is equal to ______.
If f(x) = `{{:((log_(sin|x|) cos^2x)/(log_(sin|3x|) cos x/2), |x| < π/3; x ≠ 0),(k, x = 0):}`, then value of k for which f(x) is continuous at x = 0 is ______.
Let α ∈ R be such that the function
f(x) = `{{:((cos^-1(1 - {x}^2)sin^-1(1 - {x}))/({x} - {x}^3)",", x ≠ 0),(α",", x = 0):}`
is continuous at x = 0, where {x} = x – [x], [x] is the greatest integer less than or equal to x.
If the function f defined as f(x) = `1/x - (k - 1)/(e^(2x) - 1)` x ≠ 0, is continuous at x = 0, then the ordered pair (k, f(0)) is equal to ______.
Find the value(s) of 'λ' if the function
f(x) = `{{:((sin^2 λx)/x^2",", if x ≠ 0 "is continuous at" x = 0.),(1",", if x = 0):}`
Find the value of k for which the function f given as
f(x) =`{{:((1 - cosx)/(2x^2)",", if x ≠ 0),( k",", if x = 0 ):}`
is continuous at x = 0.
If f(x) = `{{:((kx)/|x|"," if x < 0),( 3"," if x ≥ 0):}` is continuous at x = 0, then the value of k is ______.
Consider the graph `y = x^(1/3)`
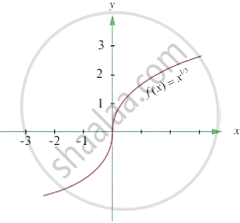
Statement 1: The above graph is continuous at x = 0
Statement 2: The above graph is differentiable at x = 0
Which of the following is correct?
