Advertisements
Advertisements
Question
Find all point of discontinuity of f, where f is defined by `f (x) = {(2x + 3, if x<=2),(2x - 3, if x > 2):}`
Solution
`f (x) = {(2x + 3, if x<=2),(2x - 3, if x > 2):}`
`lim_(x -> 2)` f(x) = `lim_("x" -> 2^-)` (2x + 3)
`= lim_(h -> 0) [2(2 - h) + 3]`
`= lim_(h -> 0) [4 - 2h + 3]`
`= lim_(h -> 0) (7 - 2h)`
`= 7 - 2 xx 0`
= 7
`lim_(x -> 2^+)` f(x) = `lim_(x -> 2^+)` (2x + 3)
`= lim_(h -> 0) [2(2 + h) - 3]`
`= lim_(h ->0) [4 + 2h - 3]`
`= lim_(h ->0) (1 + 2h)`
`= 1 + 2 xx 0`
= 1
Therefore, f is not continuous at x = 2.
APPEARS IN
RELATED QUESTIONS
Discuss the continuity of the following functions. If the function have a removable discontinuity, redefine the function so as to remove the discontinuity
`f(x)=(4^x-e^x)/(6^x-1)` for x ≠ 0
`=log(2/3) ` for x=0
Show that the function `f(x)=|x-3|,x in R` is continuous but not differentiable at x = 3.
Find the values of p and q for which
f(x) = `{((1-sin^3x)/(3cos^2x),`
is continuous at x = π/2.
Prove that the function f (x) = 5x – 3 is continuous at x = 0, at x = – 3 and at x = 5.
Examine the continuity of the function f(x) = 2x2 – 1 at x = 3.
Prove that the function `f(x) = x^n` is continuous at x = n, where n is a positive integer.
Is the function f defined by f(x)= `{(x, if x<=1),(5, if x > 1):}` continuous at x = 0? At x = 1? At x = 2?
Find all points of discontinuity of f, where f is defined by `f(x) = {(|x|+3, if x<= -3),(-2x, if -3 < x < 3),(6x + 2, if x >= 3):}`
Find all points of discontinuity of f, where f is defined by `f(x) = {(|x|/x , if x != 0),(0, if x = 0):}`
Find all points of discontinuity of f, where f is defined by `f(x) = {(x^3 - 3, if x <= 2),(x^2 + 1, if x > 2):}`
Show that the function defined by g(x) = x = [x] is discontinuous at all integral points. Here [x] denotes the greatest integer less than or equal to x.
Examine the continuity of f, where f is defined by `f(x) = {(sin x - cos x, if x != 0),(-1, "," if x = 0):}`
Find all the points of discontinuity of f defined by `f(x) = |x| - |x + 1|`.
Find the value of constant ‘k’ so that the function f (x) defined as
f(x) = `{((x^2 -2x-3)/(x+1), x != -1),(k, x != -1):}`
is continous at x = -1
Show that the function f(x) = `{(x^2, x<=1),(1/2, x>1):}` is continuous at x = 1 but not differentiable.
For what value of λ is the function
\[f\left( x \right) = \begin{cases}\lambda( x^2 - 2x), & \text{ if } x \leq 0 \\ 4x + 1 , & \text{ if } x > 0\end{cases}\]continuous at x = 0? What about continuity at x = ± 1?
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}2x , & \text{ if } & x < 0 \\ 0 , & \text{ if } & 0 \leq x \leq 1 \\ 4x , & \text{ if } & x > 1\end{cases}\]
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}x^{10} - 1, & \text{ if } x \leq 1 \\ x^2 , & \text{ if } x > 1\end{cases}\]
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}- 2 , & \text{ if }& x \leq - 1 \\ 2x , & \text{ if } & - 1 < x < 1 \\ 2 , & \text{ if } & x \geq 1\end{cases}\]
Discuss the Continuity of the F(X) at the Indicated Points : F(X) = | X − 1 | + | X + 1 | at X = −1, 1.
Prove that `1/2 "cos"^(-1) ((1-"x")/(1+"x")) = "tan"^-1 sqrt"x"`
Show that the function f given by:
`f(x)={((e^(1/x)-1)/(e^(1/x)+1),"if",x,!=,0),(-1,"if",x,=,0):}"`
is discontinuous at x = 0.
Find all points of discontinuity of the function f(t) = `1/("t"^2 + "t" - 2)`, where t = `1/(x - 1)`
The domain of the function f(x) = `""^(24 - x)C_(3x - 1) + ""^(40 - 6x)C_(8x - 10)` is
The function `f(x) = (x^2 - 25)/(x + 5)` is continuous at x =
How many point of discontinuity for the following function for x ∈ R
`f(x) = {{:(x + 1",", if x ≥ 1),(x^2 + 1",", if x < 1):}`
`f(x) = {{:(x^3 - 3",", if x < 2),(x^2 + 1",", if x > 2):}` has how many point of discontinuity
Let a, b ∈ R, b ≠ 0. Define a function
F(x) = `{{:(asin π/2(x - 1)",", "for" x ≤ 0),((tan2x - sin2x)/(bx^3)",", "for" x > 0):}`
If f is continuous at x = 0, then 10 – ab is equal to ______.
If f(x) = `{{:(cos ((π(sqrt(1 + x) - 1))/x)/x,",", x ≠ 0),(π/k,",", x = 0):}`
is continuous at x = 0, then k2 is equal to ______.
If f(x) = `{{:((log_(sin|x|) cos^2x)/(log_(sin|3x|) cos x/2), |x| < π/3; x ≠ 0),(k, x = 0):}`, then value of k for which f(x) is continuous at x = 0 is ______.
If the function f defined as f(x) = `1/x - (k - 1)/(e^(2x) - 1)` x ≠ 0, is continuous at x = 0, then the ordered pair (k, f(0)) is equal to ______.
Find the value of k for which the function f given as
f(x) =`{{:((1 - cosx)/(2x^2)",", if x ≠ 0),( k",", if x = 0 ):}`
is continuous at x = 0.
The graph of the function f is shown below.
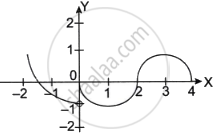
Of the following options, at what values of x is the function f NOT differentiable?
Consider the graph `y = x^(1/3)`
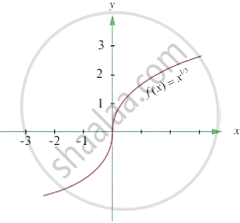
Statement 1: The above graph is continuous at x = 0
Statement 2: The above graph is differentiable at x = 0
Which of the following is correct?
