Advertisements
Advertisements
Question
Show that the function `f(x)=|x-3|,x in R` is continuous but not differentiable at x = 3.
Solution
`f(x)=|x-3|={(3-x, x<3),(x-3,x>=3) :}`
Let c be a real number.
Case I: c < 3. Then f (c) = 3 − c.
`lim_(x->c)f(x)=lim_(x->c)(3-x)=3-c`
Since `lim_(x->c)f(x)=f(c)` f is continuous at all negative real numbers.
Case II: c = 3. Then f (c) = 3 − 3 = 0
`lim_(x->c)f(x)=lim_(x->c)(x-3)=3-3=0`
Since , `lim_(x->3)f(x)=f(3)` ,f is continuous at x = 3.
Case III: c > 3. Then f (c) = c − 3.
`lim_(x->c)f(x)=lim_(x->c)(x-3)=c-3`
Since `lim_(x->c)f(x)=f(c)` f is continuous at all positive real numbers.
Therefore, f is continuous function.
We will now show that f(x)=|x-3|,x in R is not differentiable at x = 3.
Consider the left hand limit of f at x = 3
`lim_(h->0^-)(f(3+h)-f(3))/h=lim_(h->0^-)(|3+h-3|-|3-3|)/h=lim_(h->0^-)(|h|-0)/h=lim_(h->0^-)-h/h=-1`
consider the right hand limit of f at x=3
`lim_(h->0^-)(f(3+h)-f(3))/h=lim_(h->0^-)(|3+h-3|-|3-3|)/h=lim_(h->0^-)(|h|-0)/h=lim_(h->0^-)h/h=-1`
Since the left and right hand limits are not equal, f is not differentiable at x = 3.
APPEARS IN
RELATED QUESTIONS
Find all points of discontinuity of f, where f is defined by `f (x) = {(x+1, if x>=1),(x^2+1, if x < 1):}`
Is the function defined by `f(x) = {(x+5, if x <= 1),(x -5, if x > 1):}` a continuous function?
Find the points of discontinuity of f, where `f (x) = {(sinx/x, if x<0),(x + 1, if x >= 0):}`
Determine if f defined by `f(x) = {(x^2 sin 1/x, "," if x != 0),(0, "," if x = 0):}` is a continuous function?
Using mathematical induction prove that `d/(dx) (x^n) = nx^(n -1)` for all positive integers n.
Find the value of constant ‘k’ so that the function f (x) defined as
f(x) = `{((x^2 -2x-3)/(x+1), x != -1),(k, x != -1):}`
is continous at x = -1
Show that the function f(x) = `{(x^2, x<=1),(1/2, x>1):}` is continuous at x = 1 but not differentiable.
Test the continuity of the function on f(x) at the origin:
\[f\left( x \right) = \begin{cases}\frac{x}{\left| x \right|}, & x \neq 0 \\ 1 , & x = 0\end{cases}\]
Prove that the function
For what value of λ is the function
\[f\left( x \right) = \begin{cases}\lambda( x^2 - 2x), & \text{ if } x \leq 0 \\ 4x + 1 , & \text{ if } x > 0\end{cases}\]continuous at x = 0? What about continuity at x = ± 1?
Find the relationship between 'a' and 'b' so that the function 'f' defined by
In the following, determine the value of constant involved in the definition so that the given function is continuou:
Discuss the Continuity of the F(X) at the Indicated Points : F(X) = | X − 1 | + | X + 1 | at X = −1, 1.
If f(x) = `{{:("a"x + 1, "if" x ≥ 1),(x + 2, "if" x < 1):}` is continuous, then a should be equal to ______.
The domain of the function f(x) = `""^(24 - x)C_(3x - 1) + ""^(40 - 6x)C_(8x - 10)` is
How many point of discontinuity for the following function for x ∈ R
`f(x) = {{:(x + 1",", if x ≥ 1),(x^2 + 1",", if x < 1):}`
`f(x) = {{:(x^10 - 1",", if x ≤ 1),(x^2",", if x > 1):}` is discontinuous at
If function f(x) = `{{:((asinx + btanx - 3x)/x^3,",", x ≠ 0),(0,",", x = 0):}` is continuous at x = 0 then (a2 + b2) is equal to ______.
If f(x) = `{{:(cos ((π(sqrt(1 + x) - 1))/x)/x,",", x ≠ 0),(π/k,",", x = 0):}`
is continuous at x = 0, then k2 is equal to ______.
If f(x) = `{{:((log_(sin|x|) cos^2x)/(log_(sin|3x|) cos x/2), |x| < π/3; x ≠ 0),(k, x = 0):}`, then value of k for which f(x) is continuous at x = 0 is ______.
Let α ∈ R be such that the function
f(x) = `{{:((cos^-1(1 - {x}^2)sin^-1(1 - {x}))/({x} - {x}^3)",", x ≠ 0),(α",", x = 0):}`
is continuous at x = 0, where {x} = x – [x], [x] is the greatest integer less than or equal to x.
Find the value(s) of 'λ' if the function
f(x) = `{{:((sin^2 λx)/x^2",", if x ≠ 0 "is continuous at" x = 0.),(1",", if x = 0):}`
If f(x) = `{{:((kx)/|x|"," if x < 0),( 3"," if x ≥ 0):}` is continuous at x = 0, then the value of k is ______.
Consider the graph `y = x^(1/3)`
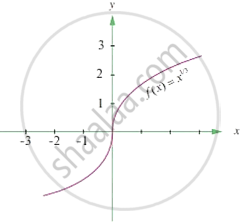
Statement 1: The above graph is continuous at x = 0
Statement 2: The above graph is differentiable at x = 0
Which of the following is correct?
